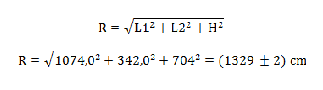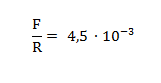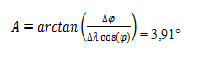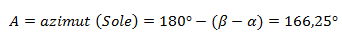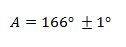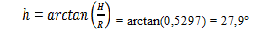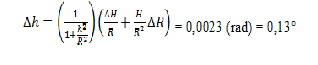|
Determinazione dell’ora attraverso il passaggio della luce solare da un foro stenopeico nella Pieve di S. Stefano in Pane di Rifredi (Firenze). Da sempre le chiese sono state eccezionali strumenti di misura del tempo grazie ai loro allineamenti geografici e grazie alla loro stazza imponente. L’orientamento geografico delle chiese e la loro mole hanno permesso per secoli di fare determinazioni del passaggio degli astri, in particolare del Sole, con ragguardevole precisione. L’edificio della chiesa è stato largamente impiegato come luogo di culto ma anche di osservazione astronomica, vista l'importanza liturgica evidenziata anche da John Heilbron (1) nel suo libro. Le chiese che hanno rivestito il duplice scopo di luogo di culto e di indagine astrometrica sono state utilizzate in tempi passati, prima che la moderna strumentazione soppiantasse la loro precisione. 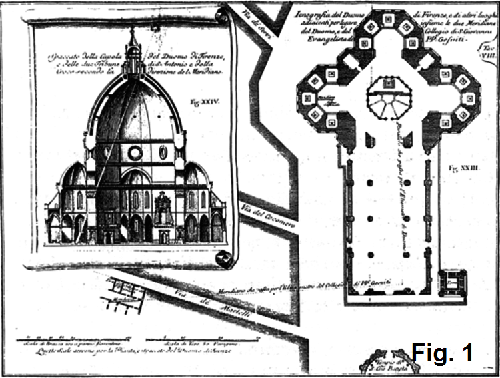 Figura 1: Pianta e spaccato della basilica di S. Maria del Fiore (Firenze) Per limitarci alla nostra città, Firenze, le chiese protagoniste in tal senso sono la cattedrale di Santa Maria del Fiore (Duomo di Firenze), con la bronzina di Paolo dal Pozzo Toscanelli posta alla base della lanterna (Fig.1), la chiesa di S. Maria Novella con la miriade di fori gnomonici realizzati da Egnatio Danti(2), il Battistero, la chiesa di S. Miniato al Monte, come ha recentemente evidenziato Simone Bartolini(3). Al giorno d'oggi le chiese come eccezionali camere oscure, con le quali effettuare valutazioni di carattere geo-astronomico, hanno perso attendibilità perché altri strumenti, più sofisticati, sono capaci di determinare con precisione assolutamente superiore gli istanti di transito di un astro, per lo più del sole. Tuttavia, nel fedele che si sofferma in raccoglimento a pregare, ancora oggi il fascino di un raggio solare che penetra da una fessura, da una finestra illuminando la pala d'altare, una formella o che semplicemente proietta la sua immagine su una nuda parete, è come allora ricco di un fascino irresistibile. Dall’esperienza di uno degli autori, riportata in fondo all’articolo, abbiamo deciso di verificare con i calcoli astronomici quanto ancora sia possibile utilizzare una chiesa per la misurazione della posizione del sole.La Chiesa La Pieve di S. Stefano in Pane si trova nel quartiere di Rifredi, un tempo in aperta campagna, oggi assorbita nella cinta periferica della città di Firenze, nella zona di nord-ovest, ai piedi del monte Morello. Il quartiere discende dalla denominazione alternativa di Rio Freddo con cui viene chiamato il Terzolle, il torrente che lo attraversa. La chiesa è inserita nel complesso denominato “Madonnina del Grappa” fondato nel secondo dopoguerra da don Giulio Facibeni, la cui statua bronzea accoglie i fedeli all’ingresso della chiesa.  Figura 2: la Pieve di S. Stefano in Pane vista da via delle Panche La pieve è attestata con certezza già dal X secolo ma è probabile che il primo edificio si debba far risalire al periodo paleocristiano, ipotesi avvalorata anche dalla dedica al primo martire della cristianità. L’aggiunta de “in Pane” nella denominazione potrebbe provenire dall’unità di misura romana degli appezzamenti di terreno, detta “panoro”, su cui era edificata la chiesa, oppure dai relativamente estesi campi di frumento posti tutto intorno, o ancora dalla presenza di un forno nei paraggi, infine dalla posizione leggermente elevata della pieve.
Figura 3: il loggiato della pieve che accoglie i fedeli prima dell'ingresso in chiesa L’attuale sistemazione è il frutto delle varie opere di ristrutturazione che si sono succedute fino alla fine del secolo scorso. L’interno è costituito da tre navate; a dividere quella centrale dalle laterali ci sono quattro arcate per parte, due a sesto acuto nella prima parte antica, rivolte verso l’ingresso e due a tutto sesto nella parte più moderna; un’ultima arcata, anch’essa a tutto sesto, è posta sopra l’altare maggiore dove cessano le navate laterali e la copertura è assicurata da una cupola a vela. La luce proviene da cinque grandi finestre con vetri dipinti posti lungo la navata destra. Poiché quella centrale ha un’altezza considerevolmente maggiore di quelle laterali, lungo le sue pareti sopra il tetto delle navate laterali c’è ancora tanto spazio per sistemare delle finestre, due per ogni arcata, strette e lunghe, parzialmente incavate che culminano con un arco a tutto sesto. Da una di esse, per la precisione dalla seconda a partire dall’abside, è penetrato il raggio di luce che ha dato il via alla nostra indagine. L’Evento
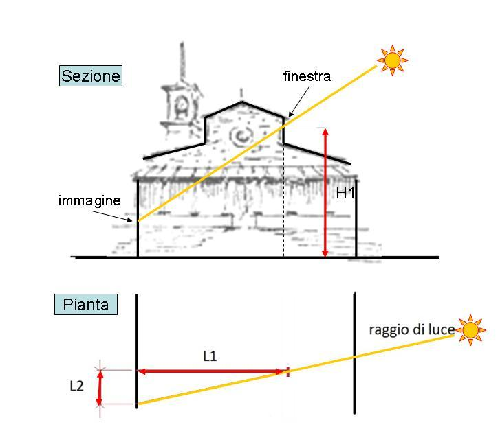
Figura 4a: particolare della navata sinistra dove si è verificato l'evento Figura 4b: particolare della navata destra da dove è penetrato il raggio solare Nel mese di ottobre, nel giorno 31 ottobre 2012, appena passate le ore 10:25 si è osservata l’immagine del sole, con le nuvole in movimento, proiettata sulla parete laterale Nord. La luce era proveniente da una finestra, parzialmente ostruita, posta nella parte superiore della navata centrale, lato opposto (Sud). Nelle due ore osservate il sole proiettato si è spostato fino oltre la porta (vedi foto 4(4)) per poi sfumare nel nulla. L’evento si è ripetuto nei giorni successivi. Le Misure Presi dalla curiosità di accertare con raffronti numerici l’evento, abbiamo ottenuto l’accesso alla chiesa dal Priore don Marco Nesti, armati di metro laser digitale e di carta e penna (nonché di una buona dose di curiosità) ed abbiamo eseguito con perizia i rilievi necessari. Abbiamo quindi misurato la distanza tra la parete Nord e la perpendicolare della parete verticale su cui è inserita la finestra (L1) e, con l’utilizzo di traguardi statici di fortuna, l’altezza rispetto al suolo del foro della finestra dal quale proveniva il raggio di luce, con l’utilizzo di traguardi statici di fortuna, l’altezza rispetto al suolo del foro della finestra dal quale proveniva il raggio di luce (H1).
Dai rilievi si ricava che: · L1 = (1074,0 ± 0,1) cm · H1 = (901,0 ± 0,6) cm · L2 = (342,0 ± 0,1) cm · H2 = (177,0 ± 0,1) cm · H3 = (20,0 ± 2,0) cm L’incertezza su L1 ed L2 è unicamente imputabile allo scarto strumentale valutato dal costruttore in cm 0,1 su 10.000, mentre all’incertezza su H1 si deve aggiungere anche lo scarto degli strumenti di fortuna utilizzati nel corso delle misure non potendo raggiungere fisicamente la finestra. L’incertezza su H3 oltre ai motivi già esposti ha l’aggravante della difficoltà nel misurare da terra la profondità dell’infisso non potendo puntare il misuratore sul foro, troppo luminoso per il riscontro visivo. H2 è invece soggetto all’unica incertezza strumentale(5). Da cui si deduce H attraverso la formula: H = H1 - H2 - H3; H = (901,0 ± 0,6) cm - (177,0 ± 0,1) cm - (20,0 ± 2,0) cm = (704 ± 3) cm Possiamo calcolare quindi la misura effettiva (R) che percorre il raggio luminoso dal foro al muro di proiezione:
Da una stima visiva si ipotizza un diametro (F) del foro di entrata della luce compreso fra 4 e 8 cm, pertanto il rapporto fra la dimensione del foro di entrata (che assumiamo pari a F = 6 cm) e la lunghezza del raggio luminoso (R) è uguale a circa:
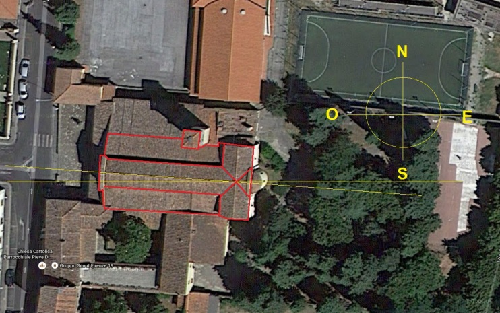
cioè il raggio luminoso compie una traiettoria di ben oltre 200 volte la dimensione del foro, il che giustifica ampiamente l’approssimazione stenopeica del fenomeno. Anche nelle condizioni estreme di un foro ampio circa 8 cm la traiettoria sarebbe sempre superiore a 150 volte l’apertura. Quindi le misure effettuate, se mai ce ne fosse stato bisogno, comprovano che l’immagine proiettata sulla parete è effettivamente l’immagine del sole e non una semplice chiazza di luce. Infatti l’autore racconta di avere visto il transito delle nuvole sul disco del sole; una semplice chiazza di luce non è capace di proiettare ciò che avviene all’esterno. Se non si fosse trattato di un foro stenopeico in occasione del passaggio delle nuvole si avrebbe avuto semplicemente un affievolimento della luminosità. Determinazione dell’azimut (A) e dell’altezza del Sole (h) Ci occupiamo innanzitutto del calcolo dell’azimut del sole e per fare questo dobbiamo calcolare l’orientamento della Chiesa (?) rispetto ai punti cardinali e del raggio di luce in riferimento alle pareti della costruzione (?). Per l’orientamento cardinale della chiesa utilizziamo Google Earth e rileviamo i valori di longitudine e latitudine di x e y : x (lato entrata chiesa) = 43°48’3,07’’ N, 11°14’26,66” E y (lato altare) = 43°48’3,00” N, 11°14’28,08” E 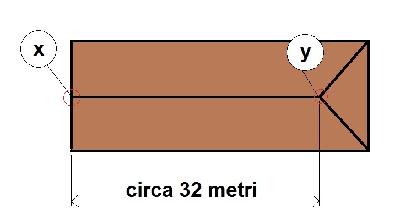 Otteniamo quindi la differenza di latitudine pari a 0,07” e di longitudine pari a 1,42”. Da ciò di deduce che l’asse longitudinale dell’edificio è orientato a EST-OVEST con un piccolo scarto verso NORD lato ingresso chiesa. Dopo aver corretto la differenza di longitudine per il coseno della latitudine del luogo abbiamo ottenuto uno scarto di
dove, nella formula, (Delta Phi) rappresenta la differenza di latitudine tra i due punti, mentre (Delta Lambda) la differenza di longitudine e (cos Phi) il coseno della latitudine del luogo.
Figura 5: foto aerea della pieve e delle strutture immediatamente adiacenti ad essa Nell’analisi degli errori che segue prendiamo come incertezze il centesimo di secondo d’arco per ciascun punto. Come riprova abbiamo voluto determinare le dimensioni della chiesa, partendo dalle differenze riscontrate di latitudine e longitudine, confrontandole con quelle rilevabili mediante lo strumento di misura delle distanze tra i due punti presenti su Google Earth. Le misure hanno confermato una coerenza nell’ambito di qualche centimetro.
La determinazione di (?) si ottiene calcolando l’arcotangente del rapporto tra L2 ed L1, ottenendo ?=17,66° Per il calcolo dell’azimut del punto dove è proiettata la figura del sole occorre quindi eseguire la differenza tra ? e ?, poiché lo scarto della posizione della chiesa è rivolto verso Nord, mentre l’orientamento del raggio luminoso (rispetto alla parete di proiezione) è rivolto verso Sud. Il sole si trova oltre la parete opposta pertanto il suo azimut (A) sarà dato dal supplementare di tale differenza. Pertanto:
Con i valori delle incertezze sopra dichiarati per le determinazioni delle latitudini e longitudini dei punti x e y otteniamo un errore su ? pari a 0,9° e con le incertezze di L1 e L2 un errore su ? di 20”. Pertanto il valore finale di azimut del Sole risulta essere:
L’altezza del sole (h) si ottiene calcolando l’arcotangente del rapporto fra l’altezza (H) e la proiezione del raggio (R) solare sul pavimento della chiesa.
Per calcolare l’incertezza su h utilizziamo le formule delle derivate parziali fatte rispetto ad H ed R,
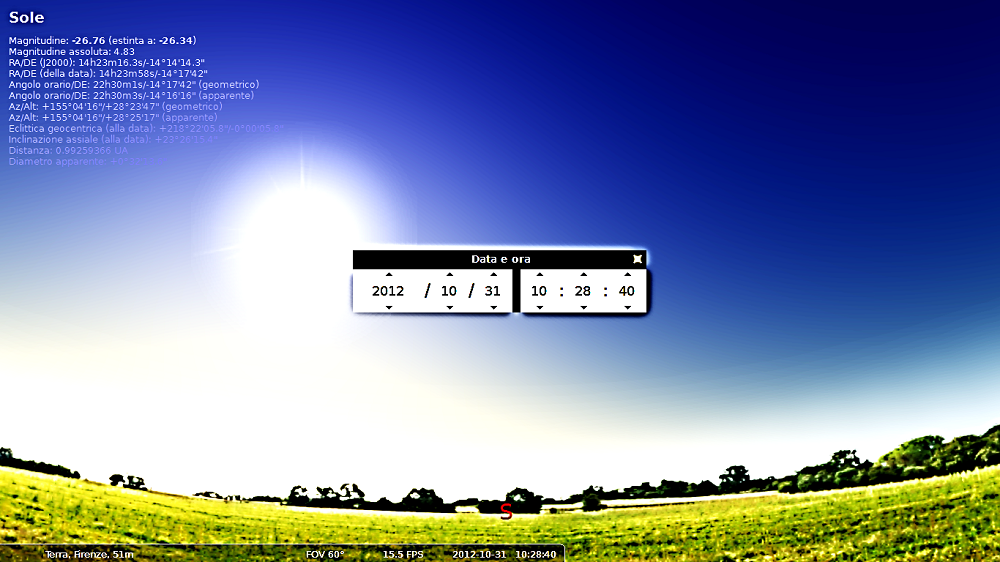
Quindi: h = 27,9° ± 0,1° Con l’utilizzo di un simulatore della volta stellata confrontiamo i dati calcolati, relativi alla posizione del Sole, con quelli espressi da Stellarium(6)(vedi figura 6) selezionando la data, l’ora ed il luogo dell’evento, prendendo in esame l’azimut e l’altezza apparenti.
Figura 6: riproduzione della configurazione celeste al momento dell'osservazione (immagine realizzata con Stellarium) Esso fornisce per il Sole: Az/Alt: +155°04'16"/+28°25'17" (apparenti) che espressi in gradi e decimali e comparati col nostro margine di errore corrispondono a: azimut = 155,0°; altezza = 28,4° Il dato calcolato dell’azimut (A), tenendo conto degli errori sperimentali, risulta sovrastimato di circa il 7%, mentre il dato calcolato per l’altezza (h) si conforma a quello reale espresso da Stellarium. Misura del tempo Con i dati a nostra disposizione possiamo tornare allo scopo iniziale della nostra ricerca, cioè determinare l’ora a partire dalla posizione del sole (A, h) sapendo il giorno dell’anno: · Il valore di azimut calcolato è compreso fra 165° e 167°, ciò permette di verificare su Stellarium che l’orario dell’evento in oggetto è compreso tra le ore 11h:05’:31’’ e le ore 11h:12’:44’’. · Il valore di altezza calcolato è compreso tra 27,8° e 28,0°, ciò permette di verificare che l’orario dell’evento ha avuto luogo tra le ore 10h:20’:47’’ e le ore 10h:23’:15’’. La differenza fra le due determinazioni di orario è abbastanza significativa ma effettuando una media pesata sugli errori, nella determinazione dell’azimut e dell’altezza, arriviamo alle ore 10h:28’:44” con un’incertezza di 1 minuto 30 secondi; l’evento deve essersi verificato cioè tra le 10h:27’:15” e le 10h:29’15”. Conclusioni
Nonostante i mezzi a disposizione per l’effettuazione delle misure nell’edificio e l’impossibilità di raggiungere fisicamente le finestrature (a circa 9 m di altezza) i risultati ottenuti coronano gli sforzi degli autori nel ricavare sia la posizione del sole, sia l’istante in cui è stato ripreso dalla foto (figura 7) mediante calcoli matematici, provando l’attendibilità di questo fenomeno astronomico. L’evento ha avuto luogo davvero entro l’intervallo orario ricavato. Uno degli autori racconta infatti di essere entrato in chiesa intorno alle 10:20 e sono trascorsi, lo dice lui stesso, almeno altri 5 minuti, prima di accorgersi del fenomeno, più una manciata di secondi per tirar fuori il telefonino e fotografare l’immagine del sole congelando l'istante. La chiesa offre a chiunque la possibilità di osservare l’immagine stenopeica del sole (tempo permettendo) nei giorni dell’anno a cavallo di quello nei quali gli autori hanno osservato il raggio di luce proiettarsi sulla parete, nonché di ripetere, migliorandoli, i rilievi, regalando a tutti la gioia provata dai sottoscritti allorquando sono stati verificati entro i limiti sopra esposti. L’esperienza effettuata
Una mattina accadde: finalmente il “segno”. Questa che segue è l'esperienza che ho vissuto, in solitaria. Il fatto che fosse in solitaria (la chiesa era deserta) nulla vale perché il “segno” è dimostrabile e ripoducibile. Ero di fretta, una mattina di pioggia nell’ultimo giorno di ottobre del 2012. Arrivai a passo veloce di fronte alla Pieve di S. Stefano in Pane; erano circa le 10:20 e, nonostante la solita incomprensibile fretta con cui mi muovo, mi volli fermare per dire una preghiera, come mi capita spesso. E altrettanto spesso mi capita di trovare i portoni delle chiese (purtroppo) chiusi, mentre quando ero bambino le chiese erano un rifugio per l'anima, in qualunque momento della giornata. Fortunatamente S. Stefano in Pane è quasi sempre aperta. Entrando vidi uscire una signora che lasciava alle sue spalle la chiesa completamente vuota. Come sempre indugiai all’ingresso con una sensazione di rispetto, attendendo che gli occhi prendessero confidenza con la penombra interna. Nel varcare quelle soglie ho sempre l’impressione di entrare in un altro tempo, in un mondo fermo, distaccato dalla fretta concitata e dai rumori esterni, e mi tornano in mente le chiese di S. Felice a Ema e del Sacro Cuore del Romito che frequentavo da bambino. Dopo essermi fatto il Segno della Croce camminai sulla sinistra, fino al punto dove le panche verticali si interrompono per lasciare il posto, in prossimità dell’altare, a quelle rialzate laterali, dove la domenica si siedono i ragazzi del coro. In quei luoghi mia figlia si è seduta qualche anno addietro in attesa di ricevere la sua Prima Comunione. Mi fermai in raccoglimento con gli occhi chiusi, godendo di quel momento ricco di piacevoli sensazioni e silenti riflessioni. Si approssimava la ricorrenza dei Santi, e nella mia mente ricordavo i miei cari affidandoli come sempre alla Provvidenza. Tutte le volte che sono in raccoglimento (come ho sempre fatto fin da bambino) chiedo al Signore un segno che manifesti la sua presenza, che rassicuri il mio percorso. E apro gli occhi per un momento, mettendomi ad osservare accuratamente in giro. Non mi aspetto certo di vedere qualcosa; la nostra stessa esistenza è di per sé un segno più che eloquente per individuare la mano Divina, ma nel modo più infantile e speranzoso possibile perlustro con lo sguardo tutta la chiesa ed in particolare le grandi finestre in alto, con i mosaici colorati, nella speranza di vedere quelle grandi lame di luce che contraddistinguono nella Bibbia la presenza dello spirito Divino. Dio è Luce, si legge.
Ovviamente non mi accade mai nulla di tutto questo. Sorridendo della mia infantile vanità abbasso lo sguardo e sulla sinistra, sul muro alla mia altezza, vedo un ovale di luce. Il cuore mi batte forte, non posso davvero credere che… mi avvicino: come su uno schermo cinematografico vedo il sole e le nuvole che gli passano davanti lentamente oscurandolo, poi tornando a luccicare, luminoso, rotondo. Meraviglioso! Il tutto proiettato da un foro in alto, sulla parete opposta da una stretta finestra a cuspide, oscurata quasi fino in vetta. Ecco; proprio da quell’unico punto non oscurato filtra il raggio luminoso che proietta il sole, come in una gigantesca camera oscura. Dopo alcuni secondi di rapimento mi scuoto e decido di filmare la scena col cellulare, dal quale vedo che sono trascorsi circa 5 minuti da quando sono entrato. Poi le nuvole vincono sulla luce e tutto diventa grigio, il sole scompare. Corro fuori a verificare la posizione del sole e lo intravedo tra le nuvole cupe di pioggia, proprio là dove mi aspettavo che fosse in base alla proiezione. La perfezione della Creazione proiettata sul muro da un’occasionale “bronzina”, come quella del Toscanelli in S. Maria del Fiore. Il “mio” segno personale dal cielo è arrivato, nel modo più teatrale e bello possibile. Con il cuore gonfio di vanagloria e convinto di aver finalmente ricevuto un “segno” molto personale, esco nel traffico piovoso e cammino spedito a circa trenta centimetri da terra. Decido di chiamare Lorenzo (mio caro amico astronomo con cui poi decidiamo di fare i rilievi e scrivere l’articolo) per condividere l’esperienza e solo molto dopo mi accorgo che sta piovendo e che non ho ancora aperto l’ombrello. Lorenzo Brandi Roberto Renzi Note. (1)J.L. Heilbron, The Sun in the Church, pubblicata nel 1999, l’autore mostra come anche all’epoca della vicenda di Galileo e nei decenni immediatamente successivi, la Chiesa sviluppò un grande interesse per le osservazioni astronomiche e la misura del tempo (2) http://www.gnomonicaitaliana.it/public/file/gnomonicaitaliana_014_export.pdf (4) Il cerchio giallo identifica la posizione del sole al momento dell’osservazione (5) Evidenziamo che H2 è stata desunta dall’immagine fotografica scattata il giorno dell’evento. (6) Assumiamo che i dati restituiti dal software siano affetti da un errore trascurabile rispetto ai nostri calcoli. |
Ultimo aggiornamento Mercoledì 04 Marzo 2020 12:49 | 
|
Desidero ringraziare il nostro Preside, Renato de Angelis, per la pubblicazione del Testamento spirituale del Maestro Salvatore Mergè, discepolo diretto di Giuliano Kremmerz e fondatore della nostra Schola. Nel suo Testamento spirituale, il Maestro Mergè ricorda spesso che un ermetista non dovrebbe pensare soltanto a cambiare il mondo, ma piuttosto prima a cambiare sé stesso, aspirando fortemente a vivere una "vita nuova". Le parole di Mergè sono davvero parole di “vita nuova”, costituiscono un tesoro grande, per il periodo che stiamo vivendo, di grandi tribolazioni, ma anche di Grande Speranza, per l’avvicinarsi alla Luce della Resurrezione Pasquale. Il primo passo da compiere sulla via dell’ermetismo, secondo Mergè, è rendersi consapevoli dei limiti propri della natura umana, tale compito non è certamente semplice, egli indica la via da percorrere nell’Amore ed in una Volontà solare, facendo attenzione a rimanere con i piedi per terra, evitando ogni forma di autoesaltazione, e mantenendo una vita esteriore piena ed equilibrata. Il Maestro Mergè, con gli insegnamenti del Testamento spirituale, ha inteso prendere per mano tutti noi, per guidarci verso il vero coronamento della ricerca ermetica, la trasformazione della nostra vita materiale, esteriore, in una “vita nuova”, spirituale, fatta di luce interiore. Egli non smette mai di metterci in guardia, avvertendo di non lasciarsi sedurre da una esistenza da superuomini, e di anelare piuttosto ad attingere alla fonte viva della spiritualità, mediante una radicale trasformazione delle condizioni del nostro modo di Essere. Con tanta lungimiranza, Mergè aveva visto bene quando diceva che il progresso materiale delle scienze sarebbe stato del tutto ininfluente, rispetto ai limiti particolari della dimensione umana, di per sé stesso, tale progresso materiale, infatti, non può in alcun modo determinarne il superamento, anzi, come stiamo assistendo in questi giorni, può al contrario essere utilizzato CONTRO l’umanità intera. Il Maestro Mergè nel suo Testamento spirituale ci ricorda che la vita umana è sacra, essa rappresenta per ciascuno di noi una grande opportunità, una leva formidabile, per risalire la china dei rimorsi, dovuti ad una materialità negativa, mettendosi al sicuro dal precipizio di un abisso d’angoscia senza fine. Ogni vita umana, dice Mergè, è espressione della Luce, creativa, della Sapienza di Dio, perciò deve considerarsi sacra, restando in contatto con la dimensione senza tempo, universale, in cui trova la sua causa prima, nei disegni dell’INTELLIGENZA DIVINA. Le nuove tecnologie non possono in nessun modo far spiccare all’uomo il “volo”, che compie, ma che può anche non compiere mai, con la generazione spirituale; questo è ciò che Mergè addita nel Testamento spirituale come il vero Miracolo da realizzare in noi. Le pagine del Testamento spirituale ci portano a meditare profondamente sulla condizione umana, siamo esseri limitati, succubi degli stimoli fisici, mentali e dei senti-menti, tutto ciò per Mergè è il frutto della misera condizione dell’uomo in stato di ignoranza e non di certo un “premio” per il servizio reso al BENE. Per la medicina odierna, non resta all’uomo che aggrapparsi alla sopravvivenza del corpo fisico, ultimo scoglio di salvezza ed unico fine della vita umana; la medicina ermetica, che Mergè conosceva bene grazie agli insegnamenti del suo Maestro Giuliano Kremmerz, guarda all’uomo nella sua integrità ed equilibrio, di corpo, anima e spirito; rivolgiamo, come il Maestro Mergè, i nostri occhi del cuore al Miracolo che può compiere in noi, in un istante fuori del tempo, soltanto la Luce di un Sole radiante. L’ETERNITÀ, scrive Mergè, è la dimora di Dio, ETERNITÀ e VERITÀ sono due degli attributi dell’ASSOLUTO; non riponiamo la Fede negli uomini, ma solo nella certezza del TUTTO UNO. Leggendo il Testamento spirituale, ci si trova proiettati di fronte alla figura di un intellettuale dalla sensibilità particolare, un autentico gigante dell’ermetismo spirituale del secolo scorso, qual è stato il Maestro Salvatore Mergè, fondatore della nostra Schola, interpretandone lo sconforto e le preoccupazioni per il destino del mondo moderno, viene spontaneo domandarsi: Nelle condizioni attuali dell’umanità, possiamo davvero ancora comprendere cosa sia la spiritualità? Siamo ancora capaci di trasformare radicalmente il nostro modo di essere per la generazione spirituale? Riusciamo a credere che esistano pratiche, in grado di donare all’uomo una maggiore consapevolezza del Creato e del Creatore? Mergè ci aveva visto lontano, additando il grave pericolo che deriva all’Umanità dalla confusione intorno alla dimensione spirituale, confusione oggi, un po’ ovunque, sotto gli occhi di tutti. Il progetto umano di un Paradiso tutto terrestre, inteso come il luogo della realizzazione di ogni desiderio materiale - come dice spesso il Preside della nostra Schola, Renato de Angelis - è una grande illusione, che l’uomo dai tempi di Adamo ed Eva non ha mai voluto abbandonare, esso porta nel suo grembo più danni per l’umanità di quanti possiamo immaginare. Insieme al primo alimento, il latte, ogni madre, dovrebbe dare ai propri figli anche un altro alimento, altrettanto essenziale alla crescita dell’uomo futuro, integro, la “Fede”. È arrivato il momento che tutti convertano il proprio Cuore, purificato dall’Amore infinito, alla Gloria che ci attende!!! L’ermetismo non è e non deve diventare un nuovo credo, come oggi da parte di molti sedicenti neokremmerziani si vorrebbe lasciar intendere; “non intendiamo fondare una religione nuova”, Giuliano Kremmerz scriveva, presentando pubblicamente la nascente Fratellanza di Myriam, egli ne aveva profetizzato bene, con lungimiranza, il pericolo di fraintendimento, e cercò con i suoi insegnamenti ai rari discepoli, tra cui Salvatore Mergè, di scongiurarne in merito ogni equivoco, anche per il futuro. Salvatore Mergè chiarisce, con il suo Testamento spirituale, ancora una volta categoricamente, che il sacrificio della pratica ermetica, è un sacrificio di Amore cristiano, fatto di tantissima Preghiera quotidiana, per il nostro prossimo e per il nostro ascenso; soltanto consacrando la nostra vita all’Amore, con la A maiuscola, egli dice, diveniamo sempre più consapevoli della necessità di dismettere gli abiti che abbiamo preso in prestito dagli elementi di questa Terra, e che formano la nostra triplice veste, fisica, psichica e mentale. Il monito di Mergè, per tutti noi, è quello di abbandonare i falsi ideali cui ci siamo aggrappati, in questa esistenza terrena, come a nuovi idoli, sacrificando sull'altare della Verità tutto ciò che pensiamo rappresenti il nostro essere, evitando il grande errore di fare di noi stessi, il nostro TUTTO. Il pensiero individuale non può determinare il nostro essere, semmai è vero il contrario, il nostro modo di essere determina il nostro modo di pensare, questo significa riconoscersi prima di ogni altra cosa, come dice il Maestro Renato de Angelis nei suoi scritti, “PURI INIZIATI, rivestiti della luce creativa d’Amore”. L'Amore infinito diviene in noi, Luce purissima, ovvero Conoscenza di ciò che è VERO; gli uomini sono gli occhi di Dio nel Mondo, come scrive Mergè, un barlume di luce riflessa dalle onde che si generano sulla superfice di un ABISSO INFINITO. La Sapienza, nei momenti di sconforto, viene in nostro soccorso, nonostante tutto non ci ha mai dimenticato, siamo noi che non gli prestiamo ascolto per la cecità dalla quale siamo oppressi, in questa epoca di suggestione collettiva. Rileggiamo con attenzione le parole del Testamento spirituale di Salvatore Mergè, meditiamone il contenuto per riceverne l’eredità spirituale. Il benessere è divenuto il credo di una nuova religione mondiale, senza Cristo, essa ci vuole tutti succubi del potere assoluto di una grande illusione, di libertà materiale, nel tentativo di renderci incapaci di accorgerci della Vera Bellezza del MONDO. Un modello di società civile, aperta a tutto indiscriminatamente, eccetto che alla spiritualità, ha preso la forma di un nuovo dogma, senza verità alcuna. L’umanità, decaduta sotto il peso del secolo scorso, passato nel culto dell’ignoranza di Dio, come Mergè aveva previsto, si ritrova oggi senza una meta, in uno stato di inazione spirituale, sospeso tra l’inerzia e la dissoluzione finale. Il più prezioso degli insegnamenti che Mergè ci ha lasciato, è quello di non perdere mai la Speranza, in quanto siamo Figli di Dio. Il mondo invecchia, la SAPIENZA resta invece immutabile, eternamente giovane, per la sua candida purezza, Essa non ha mai smesso di attenderci, perché è Amore infinito; come conclude Mergè nel suo Testamento spirituale, se solo riuscissimo a rivolgere, per un istante, lo sguardo in ALTO, saremmo capaci anche noi di nuovo di Amare, rimarremmo abbagliati, senza parole, per il Miracolo che il Vero Amore compie in noi. Salutiamo, augurando a tutti con Amore, una Felice Pasqua!
Fr+ Serio un fratello di Hermes della Schola di Salvatore Mergè  Per gli egizi, un importante elemento
costitutivo dell'individuo, in grado di estendere la propria influenza sia
durante la vita sia nel regno dei morti, è rappresentato dal cuore,
sede del Dio nell'Uomo che dell'individuo dirige il pensiero e le
attività, vivificandone il corpo. Gli antichi egizi distinguevano
nell'uomo un'intelligenza cerebrale e una innata,
detta intelligenza del cuore, che permette di penetrare la
Conoscenza delle cause e di andare al di là dei limiti animali per giungere a
quello che di Divino è nell'uomo. Facendo appello a questa coscienza
innata, soffocata dall'intelligenza cerebrale e dalla sua cultura, si
può risvegliare l'intuizione. Pittograficamente il cuore è rappresentato da un vaso munito di orecchiette (quasi a simboleggiare che per suo mezzo perviene all'individuo la capacità di intendere) ed è considerato come la sede dell'intelligenza.  Il nome attribuito dagli egiziani a
questo organo è jb nello specifico senso di sede del pensare,
del sentire ecc. Un altro nome per cuore,
che trova impiego soprattutto nei testi di anatomia, è hatj e il
Libro dei Morti parla di entrambi nel rituale “per dare il cuore
al defunto”: “Possa il mio cuore jb essere con me nella dimora
dei cuori jb, possa il mio cuore hatj essere con me
nella dimora dei cuori hatj [...] Io comprendo attraverso il mio cuore jb
ed io posseggo il mio cuore hatj.” Era quindi chiara per gli egiziani l'idea di un aspetto fisico del cuore e di una controparte spirituale, sede del pensiero, dell'intendimento, della coscienza e che adempie inoltre ad una funzione delicatissima nella vita ultraterrena, oltre a quella svolta nella psicostasia.
Tale organo rappresenta infatti anche la memoria dell'anima: “Il cuore jb della tua anima (Ba) si ricorda del tuo corpo”, chiara indicazione di come il Ba si serva del cuore spiritualizzato per “ricordare” il corpo e tornare a far visita alla mummia. Horapollo riporta che gli egiziani
consideravano il cuore, cioè l'intelligenza, e la lingua,
cioè la volontà, come i due organi creatori. Ciò è in perfetta
coerenza con la concezione teologica intellettuale di Menfi secondo la quale il
demiurgo Ptah si avvalse, nella sua opera creatrice, di Atum,
simbolo dell'intelligenza la cui sede è nel cuore e
la cui manifestazione divina è Horo, e della volontà
manifestantesi con la lingua e la cui immagine divina è Thoth. Analizzando un'antica stele del
British Museum, Junker ha potuto ricostruire la concezione secondo cui, per gli
antichi egiziani: “la visione degli occhi, l'audizione delle orecchie, la
respirazione del naso, apportano informazioni al cuore. E' lui
che fa sgorgare ogni conoscenza ed è la lingua che ripete quel
che il cuore ha pensato”. Nel Libro dei Morti, al capitolo XXVI si dichiara esplicitamente: “Io ho la conoscenza mediante il mio cuore.” (Egitto magico-religioso – Boris de Rachewiltz). Nel tempio egizio, così insegnava il Maestro al Discepolo. “Il cuore, come il Sole, è il centro del mondo; come il Sole, esso ha due aspetti: uno visibile e corporeo, l'altro percepibile solo attraverso gli effetti. E invero l'àten solare (o disco apparente) è il corpo dell'astro reale, centro delle sfere di luce, di calore e di molte altre energie. Il vero cuore
solare è la fonte di quell'energia che dà vita al nostro
mondo. Il cuore di
carne, àb, è il corpo di quel sole di vita e di Fuoco che
è il centro d'irraggiamento dell'anima BA, anima il cui aspetto
inferiore è portato dal sangue. Il nostro vero cuore
solare, centro d'attrazione del KA spirituale, è il
centro di raccolta di tutto ciò che in noi desidera quel KA e ne
accetta gli impulsi. Esso quindi può equilibrare e animare il cuore di
carne, che ne dipende e batte nella sua sfera. In tal caso il cuore
totale diventa un cuore di fuoco, un centro di Luce, una fonte di
vita che ha tutto il potere di sottomettere gli spiriti animali della
nostra personalità..” “Come la luce ardente di Râ è riflessa dalla Luna in luce fredda ed attenuata, così la visione del cuore è riflessa dal cervello. Però mentre il cuore sintetizza tutte le percezioni creandone una coscienza vitale, il cervello le separa e le fissa in determinate zone[...] Ecco perché il nome del cervello aàs è l'inversione di sàa, la coscienza del cuore. Il pensiero deve
tradurre ciò che la coscienza ha inciso nel corpo intero, ma il processo
inverso è sbagliato: se tu inscrivi nella coscienza ciò che hai elaborato
con i tuoi ragionamenti, ne risulteranno delle fantasticherie e dei sistemi
arbitrari. Tu non puoi inventare nulla; devi assimilare a te ciò che esiste
in realtà: è il rovescio della mentalità di cui il cervello è re. Affinché le mie parole risveglino in te una logica vitale e non vengano tradotte in nozioni morte, devi imparare a distinguere queste due mentalità; usa pure quella più complessa per registrare i particolari delle cose che ti si rivelano, ma sappi evitare l'analisi degli elementi 'dissezionati', perché è un'analisi che distrugge ogni legame vitale e oscura l'idea semplice originaria.”. (HerBak – Discepolo – Isha Swaller de Lubicz). A queste due mentalità mi riferivo, quando accennavo al rischio di una non corretta interpretazione dei geroglifici egizi, scrittura simbolica e sintetica, poiché per leggerne il senso profano – essoterico – è sufficiente la grammatica egittologica. Per leggerne il senso esoterico è invece necessario pensare allo stesso modo di coloro che li hanno composti e cioè con l'Intelligenza del cuore. In riferimento a quanto sopra, io sintetizzerei così: Il cuore (plesso solare) è analogo al sole come il cervello (plesso lunare) è analogo alla luna.  Gli antichi egizi sostenevano che
la “verità Una” doveva essere ascoltata con le “orecchie
del cuore” (forse “orecchiette”...) poiché se interpretata con il cervello,
grazie ai suoi “due emisferi”, l'Uno diventava immediatamente Due
e, proseguendo con il ragionamento, diveniva Quattro, Otto ecc., conducendoci
in quel “labirinto” che la sua forma rappresenta. La verità è sintesi
non analisi e serve l'intelligenza del cuore. La tradizione ha perpetuato nel tempo questa visione originaria e Geber così si esprime: “L'intelligenza ha la sua sede nel cuore poiché presiede a tutti gli organi, essa sorveglia tutto ciò che è portato al cervello dell'uomo. Senza di essa il cervello non si sarebbe svegliato”. “Quanto agli organi di animazione e rigenerazione, essi sono situati nella gabbia toracica che contiene hati, cioè il complesso cuore-polmoni, inseparabili in questa funzione. Il cuore di carne, àb, è un danzatore àb, e il suo moto di contrazione e dilatazione è il propulsore dell'attività vitale e il motore della vita animale. Il cuore regola il ritmo del flusso sanguigno. Ma il cuore, da solo, non è in grado di funzionare da motore dell'animazione: esso è coadiuvato da un organo doppio, i polmoni, in cui si incontrano il fuoco dell'aria portata dal respiro nef, e il sangue, senef. Come il fuoco non può ardere in assenza di aria, così il cuore di carne ha bisogno dei polmoni, sma, per animare il sangue e unire l'aria al fuoco. Quindi, hati è il nome della triade che fornisce l'impulso vitale organico. Il simbolo di hati è la parte anteriore di un corpo di leone, parte che comprende il cuore e il petto dal respiro possente di questo animale solare. La testa, dalla criniera tipicamente solare, completa il simbolo.” (HerBak – Discepolo – Isha Swaller de Lubicz).
Il cuore è un organo
che sta al centro del nostro corpo e che nella sua dinamica biologica pulsa per
inviare il sangue fino alla periferia del nostro essere. Il cuore, che
segna la nostra vita ma anche la nostra morte, non è solo un organo
fisiologico ma è per noi anche un simbolo sempre eloquente, perché con questa
parola ci riferiamo a una realtà molto più ampia di un muscolo decisivo per la
nostra vita. Sì, il cuore è da noi sentito come l’organo centrale della vita
interiore, come la fonte delle espressioni multiformi della vita spirituale e
per questo è situato, per così dire, nell’io profondo. Quando nel nostro contesto socio-culturale si parla di cuore, si allude innanzitutto alla vita affettiva, alle emozioni, ai sentimenti che hanno nel cuore la loro sede: “Il nostro cuore ama o odia, il nostro cuore è tenero o è chiuso, il nostro cuore accoglie o respinge”, siamo soliti dire. Nel linguaggio biblico, invece, il cuore ha un significato molto più esteso perché designa tutta la persona nell’unità della sua coscienza, della sua intelligenza, della sua libertà: il cuore è la sede e il principio della vita psichica profonda, indica l’interiorità dell’uomo, la sua intimità ma anche la sua capacità di pensiero; il cuore è la sede della memoria, è il centro delle operazioni, delle scelte e dei progetti dell’uomo. In una parola, il cuore è l’organo che meglio rappresenta la vita umana nella sua totalità. Il cuore è il “sito” spirituale della presenza di Dio (e per questo è detto tópos toû theoû nella tradizione bizantina, domus interior in quella latina), è il luogo dove Dio parla, educa, giudica, si fa presente e abita in colui che, appunto, gli “apre il cuore”: espressione, quest’ultima, significativa per dire come e dove accogliamo la presenza di Dio, come ci disponiamo alla comunicazione e all’amore. Sull'argomento sono state scritte
intere biblioteche. Vediamone in sintesi alcuni aspetti. Ma cos’è il cuore e cosa rappresenta? Sacro, unità, amore,
sensualità, unione, passione, legame, compassione, carità, verità.
A livello fisico, il
cuore è, com’è noto, l’organo essenziale per la vita grazie alla sua funzione
di pompa incessante. Il nostro corpo pulsa in base al suo ritmo e quante
informazioni potremmo ricavare dall’analisi del suo battito, che parla di noi.
Si dice che un battito cardiaco rapido e intenso corrisponda a una personalità
energica, forte, determinata. Al contrario, un battito lento corrisponderebbe a
una personalità altrettanto tranquilla e posata.
E non possiamo
dimenticare il ruolo di primo piano che il cuore ha in ambito spirituale,
quale organo sacro. Se in India in esso
risiede Brahma, i musulmani lo considerano trono di Dio, mentre le frange
esoteriche dell’Islam, come i sufi, paragonano la visione spirituale all’occhio del
cuore. Ed è sempre il cuore che nell’antico Egitto
veniva pesato per capire se il defunto fosse degno di un aldilà appagante. In antico Egitto i
saggi erano soliti parlare di intelligenza
del cuore, facendo riferimento all’intuito, quale tramite
fra conscio ed inconscio, psiche e corpo.
Analizzandolo nel
dettaglio, soffermandoci sul colore, la forma, la consistenza, si può notare
che il cuore è rosso, caldo ma al tempo stesso oscuro e cavo. Queste caratteristiche
apparentemente in contrasto tra loro lo
rendono sintesi del maschile e femminile, luogo di conciliazione dei principi
complementari. Ma il cuore è spesso associato anche al Sole e questo è dovuto
alla funzione che svolge: come il Sole è il centro del sistema solare, il suo
cuore pulsante, così il cuore nel corpo umano assolve a una funzione simile, ci
riscalda e ci tiene in vita. Ecco perché capita talvolta di vederlo raffigurato
con raggi luminosi o fiamme. Il chakra del cuore, o Anahata, si trova al centro del petto e fa da collegamento fra i 3 Chakra inferiori e i 3 superiori. Esso è la sede dello spirito, del Sé superiore, della scintilla divina che appartiene a tutti noi. L’amore ha origine in questo chakra, ovviamente non solo l’amore di tipo romantico che talvolta assume caratteristiche di possessività tutt’altro che amorevoli. No, l’amore dell’Anahata è puro, autentico, compassionevole. Il colore dell’energia del chakra del cuore è verde, in quanto simbolo di equilibrio, di armonia e di unione. Quando questo chakra è chiuso, si dice provochi indifferenza, diffidenza, insofferenza nei confronti dell’amore, cosa che comporta poca empatia nei confronti altrui ma anche verso se stessi. Sul piano sottile, esiste un piccolo spazio
misterioso accanto ad Anahata Chakra chiamato Cuore Spirituale. I grandi Maestri iniziati lo hanno collocato
nella parte destra del petto a circa un centimetro
dal cuore fisico: è una zona di proiezione dello spirito e allo
stesso tempo la sede della coscienza del Sé Divino, Atman.
Il nostro cervello non abituato alle luci
e alle ombre dei simboli, non può capire, e mai capirà, il loro significato
recondito, deve capire la base, quello sì, imparare a fidarsi e, al momento
opportuno, quando esso sarà pronto a “spegnere” la propria bramosia di
possedere, a lasciare il posto al cuore che è l’unica porta
ermetica che possiamo mai veramente attraversare. Il terribile e
temibile guardiano della soglia,
dunque, chi è se non il nostro cervello. Noi con tutto il nostro
essere cerchiamo di lasciarci andare ed attraversare la porta della
spiritualità, della luce ma lui è lì costantemente a tenderci tranelli, a darci
illusioni, a crearci confusione. Esso ha paura, ha paura di non sopravvivere in un mondo in cui il
calcolo e la misura sono inesistenti, in cui tutto è visto e non analizzato, in
cui il confine è solo una sensazione, non una quantità di qualcosa. Gli ermetisti
che hanno attraversato questa soglia, da quel giorno iniziano a capire i
simboli, senza per forza misurarli: la misura, ovvero la spiegazione razionale
dei simboli, non è contemplata nella loro ricerca, essi sono passati ad un
piano nuovo di visione, in cui percepiscono il colore, il profumo, il gusto ma
non hanno bisogno di analizzarli perché ormai hanno compreso che il segreto non
si cela nella sua conoscenza bensì nella sua capacità di utilizzarli. La natura non può essere conosciuta fino in fondo: per esempio, non è
necessario che conosca il fuoco a livello di reazione chimica, per poterlo
utilizzare, è sufficiente infatti che sappia come fare a crearlo.
Il lavoro del mago
è un lavoro simbolico su se stesso, il cervello è importante sì
per questo lavoro ma più ancora lo è il cuore. (Il Cervello e il
Cuore – I Fratelli di Hermes – S. Mergè). Il Cuore dal punto di vista scientifico
L'apparato
circolatorio è l'apparato del corpo umano deputato al corretto
funzionamento della circolazione sanguigna ed è composto da una pompa, cioè
il cuore, che è l'organo
più importante di questo sistema, e da una serie di tubi che raggiungono ogni
area ed ogni organo del corpo, cioè i vasi
sanguigni, distinti in arterie, vene, capillari e linfatici. La circolazione del sangue è fondamentale per l'organismo poiché è tramite essa
che ad ogni singola cellula del corpo vengono forniti ossigeno e sostanze
nutritive, quindi aminoacidi, zuccheri e grassi.
Questa viene resa possibile dall'azione del cuore, che è un muscolo cavo che
attraverso le sue contrazioni, spontanee e ritmiche, fa circolare il sangue in
due differenti circuiti: quello polmonare, o piccola
circolazione, e quello sistemico, o grande circolazione. Attraverso la piccola
circolazione, il sangue venoso, quindi che trasporta anidride carbonica, viene
pompato dal cuore verso i polmoni
dove si scarica, si purifica, carica ossigeno e poi torna al cuore. Da qui
riparte per la grande circolazione, cioè viene immesso nelle arterie e
raggiunge ogni parte dell'organismo, dove cede l'ossigeno e prende l'anidride
carbonica. A questo punto, torna
verso il cuore attraverso le vene,
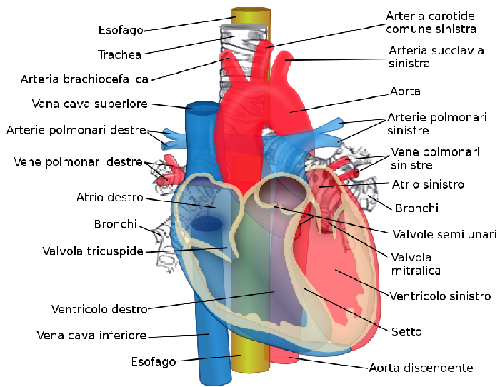
rientra nel circuito polmonare e ricomincia da capo il suo viaggio. Sangue venoso e sangue arterioso non entrano in contatto: il cuore, infatti,
sezionato in senso longitudinale appare nettamente distinto in due aree, divise
da un setto verticale. La parte destra viene
chiamata cuore venoso, perché
qui passa il sangue venoso, quella sinistra è il cuore arterioso, dove circola il sangue arterioso. Se invece lo si
considera rispetto alla parte superiore e inferiore, si vedrà che sopra ci sono
due cavità chiamate atri e
sotto altre due cavità chiamate ventricoli. Ora qualche novità scientifica. C'è sempre stato questo paradosso: quando viene concepito un bambino, il cuore umano inizia a battere prima che il cervello sia formato. Ciò ha portato i medici a chiedersi da dove provenga l'intelligenza necessaria ad avviare e regolare il battito cardiaco. Con sorpresa del mondo medico, gli scienziati dell'HeartMath hanno scoperto che il cuore ha il proprio cervello e sì, un autentico cervello con vere e proprie cellule cerebrali. È molto piccolo, ha
soltanto all'incirca quarantamila cellule, ma è un cervello e ovviamente ha
tutto ciò di cui il cuore ha bisogno. Questa è stata una scoperta di enorme
importanza e conferma la veridicità delle affermazioni di coloro che per secoli
hanno parlato o scritto sull'intelligenza del cuore. Gli scienziati dell'HeartMath hanno
fatto una scoperta forse ancora più grande riguardo al cuore. Hanno dimostrato
che il cuore umano genera il campo energetico più ampio e potente
di tutti quelli generati da qualsiasi altro organo del corpo, compreso il
cervello all'interno del cranio. Hanno scoperto che questo campo
elettromagnetico ha un diametro che si estende dai due metri e mezzo ai
tre metri, con l'asse centrato nel cuore.  Riporto
qui di seguito alcuni stralci tratti da “L'Arte di divenire simile agli Dei”,
scritto dal Maestro Eliah Elis
(Salvatore Mergè): “Rendi
ricettivo l'orecchio del cuore affinché possa ascoltare le
emanazioni dell'organo misterioso riattivato; l'uomo possiede facoltà
straordinarie che lo rendono uguale agli Dei, se solo saprà togliere da se
stesso ogni imperfezione. Tu, figlio mio, possiedi una rete sottilissima che
collega tutti gli organi, e in tale rete passano le molteplici vibrazioni
vitali; non dimenticare che tu stesso sei il laboratorio alchemico nel quale
procede l'opera della tua trasmutazione”. “L'educazione
del cuore avviene durante l'attività del fuoco che rende il corpo
fluido e malleabile agli impulsi dello spirito”. “Avendo
raggiunto il cuore fluidico e il contatto con il Maestro
che esprime il potere centrato nel cuore, risveglierai la potenza
fluidica e irradiante in quanto il tuo io, trasferito nel mondo immateriale, si
staccherà e si isolerà dalla componente fisica”. “Molto
importante per te è lasciare aprire il tuo cuore, perché le sue
pulsazioni sono in armonia con quelle del cosmo, il quale è un'Entità che vive
in noi, e noi in esso”. Il Kremmerz, parlando della memoria, accenna alla grande differenza che vi è tra il “ri-membra-re” ed il “ri-cor-dare”, ovvero, tra la nostra memoria del corpo e della nostra vita attuale e quella del cuore e dell'uomo storico, o antico, delle nostre vite precedenti, che è in noi. Vorrei concludere con un modo di dire espresso dal Maestro Kremmerz in una sua lettera per significare la sincerità: “[...] parlare con il cuore in bocca [...]”. Dua-Kheti Bibliografia: - Egitto
magico-religioso – Boris de Rachewiltz - HerBak – Discepolo
– Isha Swaller de Lubicz - avvenire.it-cuore –
Enzo Bianchi - Il Cervello e il
Cuore – I Fratelli di Hermes – Salvatore Mergè - benessere.com - Cuore - scienzaeconoscenza.it
– Un cervello nel cuore   La conoscenza della
ghiandola pineale e l’associazione con il cosiddetto terzo occhio” (l’occhio interiore che
tutto vede) risale a tempi molto antichi e possiamo trovarne rappresentazione
in varie culture nel corso della storia umana. Ci è possibile
riscontrarla in alcune immagini, come l’occhio di Ra degli antichi egizi (che
rappresenta proprio l’epifisi nella sezione del cervello), oppure rappresentata
in opere architettoniche spirituali (come la “pigna” del Vaticano), negli
antichi reperti come quelli degli Anunnaki o nelle
rappresentazioni del Buddha. Il terzo occhio viene anche chiamato Occhio centrale di Shiva o Occhio di Horus.  Una domanda nasce spontanea: perché la ghiandola pineale viene rappresentata in modo così evidente in tantissime culture nella storia dei tempi? Forse è un’informazione importante da tramandare? Forse rappresenta veramente la connessione tra il mondo visibile e quello invisibile? Gli studiosi di religioni orientali riconoscono
al Terzo Occhio una lunga tradizione in India, Cina e Asia, dove
l’induismo, il buddismo e il taoismo dominano. Stranamente, il Terzo Occhio
viene ignorato dagli archeologi delle culture del Nuovo Mondo, nonostante ampie
prove del suo simbolismo siano presenti nell’arte delle antiche culture
americane. Troviamo questo simbolismo del terzo occhio tra
le culture che si sono evolute negli attuali Messico, Perù, Colombia, Panama e
persino Stati Uniti (vale a dire i popoli Olmechi, Toltechi, Maya, Zapotec, Aztechi, Inca e pre-Inca, tra
gli altri).
La ghiandola
pineale fu scoperta più di 2300 anni fa dallo scienziato alessandrino Erofilo. La prima descrizione e le prime speculazioni
su di essa si trovano nei voluminosi scritti di Galeno che trattò
la ghiandola pineale nel suo De usu partium. In esso Galeno spiega che la ghiandola deve il suo nome alla sua
somiglianza, per forma e dimensioni, a un pinolo. Nel 1600 Cartesio la definì sede dell’anima. Biologia e funzione della ghiandola pinealeLa ghiandola
pineale o epifisi (dal
greco epi-fysin, che significa al
di sopra della natura) ha una forma simile ad una piccola pigna, da cui deriva il nome “pineale”; (pinea è
il termine latino corrispondente a pigna). Ogni essere vivente,
mammiferi inclusi, mantiene l’equilibrio biologico–metabolico a
partire dai ritmi e dalla periodicità circadiana
giorno–notte e tali ritmi planetari determinano la sintesi e la
secrezione circadiana degli ormoni ipotalamici e ipofisari secondo una ritmicità
legata alla rotazione terrestre e lunare. La sincronicità della
secrezione ormonale è fondamentale per la salute; la sua risincronizzazione è
la base di ogni intervento di prevenzione e la cura di praticamente tutte le
patologie. La ghiandola pineale svolge un ruolo primario in questa sincronicità. La pineale è il principale
organo del corpo umano responsabile del controllo del ritmo biologico circadiano,
sulla base del principale ritmo cosmologico, quello dell’alternanza luce-buio.
L’attività endocrina della pineale inibisce l’ipotalamo e, indirettamente,
l’ipofisi ed altre ghiandole.
L'attività secretoria
della ghiandola pineale presenta delle alterazioni ritmiche
legate alla luminosità dell'ambiente, raggiungendo i valori massimi al
buio e i valori minimi con la luce diurna.
La ghiandola
pineale è una ghiandola endocrina di circa 150 grammi, grande circa
quanto un pisello o una nocciola, incastonata in profondità dentro il cervello
dei vertebrati. Si trova, in effetti, proprio vicino al centro del
cervello, tra i due emisferi, all'estremità posteriore del terzo
ventricolo; è collegata mediante alcuni fasci nervosi pari e simmetrici
(peduncoli epifisari) alle circostanti parti nervose. È nascosta in una
scanalatura a cui aderiscono i due corpi arrotondati dell’ipotalamo, a cui la
pineale afferisce e che la rendono, così, una delle parti più protette
del corpo. Proprio perché così
protetta, l’epifisi è una struttura che, fino a poco tempo fa, era
stata poco studiata, benché tenuta in grande considerazione: essa era infatti
conosciuta fin dall'era antica anche per la sua frequentissima calcificazione
in età matura, tanto da essere considerata la chiave per comprendere il
processo d’invecchiamento. La pineale controlla infatti l'orologio biologico del corpo,
“l’organizzazione circadiana” che determina il ciclo giornaliero del sonno e
della veglia. Ma essa non regola solo i ritmi del sonno, bensì il ritmo della
vita stessa, come appare più chiaramente nel regno animale: qui, in
primavera, la pineale riaccende le pulsioni sessuali; in autunno
segnala agli uccelli che è tempo di migrare, funzionando anche come una bussola
fisiologica che li mantiene sulla giusta rotta di volo; in inverno
avverte gli animali che è tempo di cercare un riparo e di entrare in letargo. Negli esseri umani,
il ruolo della pineale è più sottile ma ugualmente importante. Essa è
definibile come il “regolatore dei regolatori” che sovraintende
alle operazioni di tutte le altre ghiandole,
aiuta a mantenere nella norma i livelli giornalieri e stagionali degli
ormoni e presiede alla crescita e allo sviluppo, dall'infanzia fino all'età
adulta. L’epifisi
esercita il suo controllo attraverso una molecola chiamata melatonina (Melas = Nero; Tonos = Tensione):
si tratta di un ormone che regola il ritmo circadiano di sonno e veglia,
reagendo al buio o alla poca luce. La ghiandola pineale secerne difatti
melatonina solo di notte: poco dopo la comparsa dell'oscurità, le
sue concentrazioni nel sangue aumentano rapidamente e raggiungono il massimo tra
le 2 e le 4 di notte, per poi ridursi gradualmente all’approssimarsi del
mattino. L’epifisi produce la melatonina tramite alcune cellule pigmentate, i "pinealociti",
che sono simili alle cellule pigmentate della retina; esse
rendono la ghiandola sensibile alla luce e pronta a reagire all'alternanza
periodica di luce e di buio, recepita e trasmessa dall’occhio. La melatonina è, in definitiva, lo strumento che l’epifisi
utilizza per definire tutti i ritmi umani, giornalieri e a lungo termine,
dall'infanzia in poi. Tale ormone è peraltro già presente nella vita
intrauterina: attraverso la placenta, la melatonina passa infatti dalla
madre al feto. I bambini, pur non producendo la loro riserva di melatonina
prima del terzo o quarto giorno di vita, la assorbono tramite il latte
materno.
La melatonina
viene sintetizzata da due sostanze: il triptofano e la serotonina.
Quest’ultima è un neurotrasmettitore impiegato nella regolazione della
temperatura del corpo, del senso di fame/sazietà e dell’umore è infatti soprannominata
anche “l’ormone della felicità”.
L’aspetto più
interessante della ghiandola pineale, tuttavia, è la produzione
di un’altra molecola: la DMT (Dimetiltriptamina), un neurotrasmettitore chiamato anche “la molecola dello Spirito”
che ha particolari funzioni legate principalmente al “collegamento” tra
il corpo e lo Spirito. Studi scientifici
hanno dimostrato come l’epifisi secerne spontaneamente grandi
quantità di DMT in due
particolari momenti della vita: la nascita e la morte (o anche
durante le esperienze di premorte). Questo a dimostrazione del fatto che la DMT fa da “ponte” tra il corpo fisico e il mondo spirituale. In alcune persone,
anche durante il sonno, la ghiandola pineale secerne una
sufficiente quantità di DMT, tale da rendere possibili
esperienze particolari come i sogni lucidi o i viaggi astrali. In poche
parole, la ghiandola
pineale è il collegamento con il mondo invisibile o il mondo dello Spirito, argomento che gli sciamani, ad
esempio, conoscono molto bene. Forse avrete sentito
parlare dell’Ayahuasca.
Nella lingua quecha, che si parla in Ecuador, Perù, Bolivia e Colombia, aya significa spirito e huasca significa vite. La parola Ayahuasca viene quindi tradotta col termine vite ( vino ) degli spiriti. L’Ayahuasca è un decotto ottenuto attraverso una lenta ebollizione di due piante: una liana, detta Banisteriopsis caapi, ed un arbusto noto come Psychotria viridis, utilizzato come allucinogeno nelle cerimonie sciamaniche per indurre stati di coscienza alterati a scopi terapeutici, il cui principio è proprio la DMT.  Il “terzo occhio”
(o sesto chakra) E’ interessante notare che in India la parola “chakra”
deriva dalla parola sanscrita per “ruota” o “curva”
ed è legata alle parole “vortice” o “mulinello”. Queste parole implicano fondamentalmente, un
cerchio con un punto al centro. Questo è degno di nota perché molte rappresentazioni
del Terzo Occhio, nell’antica arte americana, utilizzano un “cerchio
puntato”. Dal punto di vista
esoterico/spirituale, la
ghiandola pineale rappresenta il famoso “terzo occhio”,
ovvero l’occhio dell’Anima che è in grado di vedere la realtà,
che non è quella che appare ai nostri occhi fisici ma quella più “sottile”,
celata dal “velo di maya”. Il terzo occhio è
in grado di “vedere” l’invisibile, di vedere al-di-là
della vista ordinaria, di percepire quella realtà che gli occhi umani non colgono
(sembra infatti che la percezione dei sensi ordinari sia limitata ad una minima
percentuale di ciò che esiste).
Esso, nelle antiche tradizioni induista e buddista,
corrisponde al sesto chakra (Ajna) situato al
centro della fronte tra le sopracciglia. Questo centro rappresenta l’occhio
interiore in grado di percepire la realtà oltre la visione ordinaria, è
la porta della chiaroveggenza e della visione superiore. Il terzo occhio è la
connessione con la propria mente intuitiva, con il Sé
Superiore, diciamo pure con la propria Anima.
Addirittura Cartesio sosteneva che la ghiandola pineale fosse proprio la sede della coscienza: nel suo libro “Le passioni dell’anima” descrive il ruolo della ghiandola pineale, appunto, come la sede principale dell’anima, nella quale la "res extensa" si unisce alla "res cogitans". Comunque,
in tutte le tradizioni spirituali, la “visione” del terzo occhio ha un ruolo
fondamentale nella connessione
dello Spirito con l’uomo. Esso ci permette infatti di
entrare nel mondo del “non materiale”, dell’apparentemente invisibile
attraverso la percezione extra-sensoriale, per portarci conoscenza, profonda
consapevolezza e ci consente di “guidare” la nostra esistenza. Per questo è importante mantenerlo attivo e in uno stato funzionale.  Rick Strassman, psichiatra
dell’Università del New Mexico, iniziò a fare esperimenti sulla “dimetiltriptamina”,
altrimenti detta DMT, che, come abbiamo già visto, è una sostanza
particolare presente sia in natura (in piante come l’Ayahuasca) sia
nel cervello umano, prodotta dalla Ghiandola Pineale. Strassman
aveva come finalità della sua ricerca l’utilizzo della sostanza psicotropa a
fini terapeutici. I pazienti a cui veniva somministrata la molecola sotto
stretto controllo riferivano di viaggi astrali e contatti sconvolgenti con
“altre realtà” non meno reali della nostra, abitate da esseri sovrannaturali. La DMT rilasciata naturalmente
dalla Ghiandola Pineale si pensa faciliti il movimento dell’Anima
all’interno e fuori dal corpo e sia parte integrante dei più alti stati di
meditazione e di esperienze mistiche. Con il termine “Terzo Occhio”,
riferito alla suddetta Ghiandola Pineale, si vuole rappresentare
il nostro “Sesto Senso”. Quante volte abbiamo sentito nominare il “Sesto
Senso”? Se avete una buona conoscenza riguardo i Chakra,
noterete che proprio il sesto denominato Ajna in
Sanscrito è la sede del Chakra del Terzo Occhio ove giacciono
tutti i sensi interiori. Esso permette la comunicazione con lo Spirito.
Negli individui in cui questa è molto sviluppata, permettendo, quindi,
di percepire energie sottili, sia riguardo il campo visivo che uditivo, si manifesta
la Chiaroveggenza. La Ghiandola Pineale produce da
sé questa molecola particolare dal nome DMT senza il bisogno di
utilizzare altri tipi di sostanze. Per far sì che essa si decalcifichi,
necessita effettuare un profondo lavoro su se stessi. Secondo Strassman, la DMT sarebbe la sostanza per
eccellenza in grado di aprire un “portale” verso universi e dimensioni
parallele che coesistono con la nostra realtà ma che non siamo in grado
di captare o decodificare, appunto, perché filtrati dalla valvola rappresentata
in primis dal nostro cervello, costretto a trasmettere soltanto
il “canale normale”, quello del mondo di tutti i giorni. Secondo la fisica moderna infatti
esisterebbero un numero incredibilmente elevato di universi paralleli, o
multiversi, ciascuno dei quali simile al nostro e soggetto alle stesse
leggi fisiche ma, al contempo, “alternativo” a causa della diversa composizione
delle particelle che lo costituiscono.  A proposito del “sesto
senso”, il Kremmerz così scriveva: “La libertà del
potere centrale intellettivo si guadagna attutendo la sensibilità fisica
dell'uomo. I mezzi di pratica
per la intuizione della verità ultra umana si riducono a uno: Ridurre inerti i
sensi animali per dare completa libertà all'altro, al senso che è
il medio conduttore tra l'ultra umano e l'umano. Questo mondo di là,
questo mondo di esseri già vissuti o non mai vissuti nella vita terrena non si
può né apprezzare né giudicare coi mezzi ordinari del controllo dei sensi
animali; ed è inutile volerlo far credere esistente a chi non ha sviluppata
quella proprietà speciale che è l'occhio dell'anima e che abbiamo
chiamato sesto senso o percezione sottile o telema
o mercurio intellettuale. Come nel mondo delle
forze meccaniche così nell'iperfisico, ogni azione genera una reazione.
Ora nelle forze, nelle creature e nelle intelligenze che popolano il mondo
invisibile, l'azione è opera dell'intuente, o meglio di chi ha sviluppato il sesto
senso, percependo presente l'azione delle forze e delle intelligenze iperfisiche,
la reazione delle quali colpisce il mondo fisico.
La Ghiandola Pineale influisce sui nostri sogni Abbiamo visto che dal punto di vista biologico, la ghiandola
pineale produce la melatonina che ha lo scopo principale di regolare il
ritmo circadiano, ovvero le fasi del sonno e della veglia. Abbiamo visto che la sua attività secretoria
raggiunge valori massimi al buio e minimi con
la luce. Abbiamo anche visto che essa produce un'altra
importante molecola, la DMT, che per la sua particolare virtù di “ponte” tra il corpo fisico e il mondo spirituale è
chiamata “la molecola dello Spirito”. Seguendo il sentiero che ci conduce al sonno, al buio e superato il
“ponte”, sotto il
quale scorre il fiume edenico con la ”molecola dello Spirito”, giungiamo
nel fantastico mondo dei sogni.
Secondo alcune ricerche, è stato confermato che ci sono alcuni periodi della notte, tra le ore una e le ore quattro del mattino, durante la fase REM dei sogni, in cui alcune sostanze chimiche vengono rilasciate nel cervello e agiscono sui nostri sentimenti, facendoci connettere con la nostra fonte superiore. Alcuni la chiamano coscienza, altri spirito, altri ancora anima, corpi sottili o altri semplicemente la chiamano ego.
E’ un argomento
complicato per certi versi, sta di fatto che quando una persona dorme e quindi “sogna”
non utilizza la mente razionale, ma semplicemente lascia scorrere per qualche
ragione le immagini. Ad esempio, se sognate un leone o una tigre, anche se
potete reagire in vari modi, tipo scappare o accarezzare l’animale, osservarlo,
urlagli contro, etc,… il vostro corpo non reagirà mai come se foste realmente
davanti ad un’animale pericoloso, e questo accade perché (quasi per tutti, a
parte per le menti allenate) nei nostri sogni facciamo da spettatori.
Se ci fate caso non possiamo far nulla, non possiamo decidere cosa fare in un
sogno, accade quello che deve accadere. Una delle tante potenzialità che ha la nostra ghiandola pineale, una volta “risvegliata”, è riuscire a controllare i propri sogni.
Cosa vuol dire? In pratica non facciamo più da spettatori nei nostri sogni, ma
da “attori protagonisti”: in altre
parole, non faremo altro che “prendere coscienza” delle nostre
azioni. Terminiamo questo nostro percorso con qualcosa
che risvegli in noi il nostro spirito di fanciullo e cioè una “favola”.
Forse non tutti sanno che il “Pinocchio” di Collodi è un racconto iniziatico velato sotto forma di favola
per bambini. Già il nome Pinocchio deriva dalla
composizione delle parole “pino” e “occhio”. Il pino è
l’albero i cui frutti, i pinoli, hanno la stessa forma della ghiandola pineale, che nella
tradizione esoterica rappresenta appunto il “terzo occhio”. Pin-occhio
(occhio-pineale) è pertanto una chiara allusione alla ghiandola pineale, cioè la manifestazione fisica del “terzo occhio”.
Pin-occhio
(l’occhio della pineale) è a tutti gli effetti la rappresentazione del percorso
di risveglio. Il Padre, Geppetto, ne è il Creatore,
infatti non è un vero padre nel senso comune del termine ma Colui che lo
trae dalla materia e gli dà forma. Pinocchio non nasce da una donna e questo è il primo fatto
extra-ordinario. Geppetto lo scolpisce nel legno, lo crea burattino, cioè un essere
“meccanico”, “addormentato”, in grado di parlare e camminare ma non
dotato di coscienza, quindi non ancora umano. Appena creato, Pinocchio
diviene subito ingestibile, in quanto non ha ancora ritrovato
né la sua anima (la
Fata Turchina) né tanto meno il Padre, dal quale dovrà prima separarsi per conoscere le insidie del mondo,
proprio come accade al figliol prodigo nell’omonima parabola evangelica. Lungo
il suo cammino iniziatico impara a conoscersi, a gestire il corpo, le
emozioni e la mente, sorvegliato a distanza dalla sua anima, la quale –
nonostante le menzogne del burattino – lo aiuta nei momenti più bui e lo
rimette sempre sulla “retta via”.
Un pezzo
di legno, un burattino per l’appunto, a cui viene insufflata
un’anima e prende vita, ma che con varie prove (iniziatiche) riuscirà
alla fine a diventare un “Bambino Vero”. Facile comprendere che il pezzo di legno animato, dotato di vita quindi, ma senza Volontà in quanto burattino è un’allegoria del sé inferiore, mentre il Bambino Vero (Bambin Gesù) rappresenta la nascita del Cristo nell’uomo o Sé Superiore.
Dua-Kheti Bibliografia: Visione olistica – La Ghiandola Pineale – Terzo
occhio Neovitruvian – Il terzo occhio nelle antiche
culture occidentali Neuroscienza – La ghiandola pineale KarmaNews – La pineale e gli ormoni della
sensitività Psicologi Italia – Dr. Andrea Napolitano – La
ghiandola dell'anima Hackthematrix - DMT e Ghiandola Pineale – Maya Hikari
Coscienza Universale – Ghiandola pineale
influisce sui nostri sogni PRESENTAZIONE Ho
trovato davvero straordinario questo articolo sulla
concezione che avevano i primi egiziani del cuore umano e del Cuore di Dio e
desidero condividerlo con tutti i fratelli ed i lettori del sito della Scuola
Ermetica “Salvatore Mergé”. L’autore,
francese di nascita, Louis Charbonneau-Lassay, è stato, per quello che a noi
qui più interessa, un esperto incisore ed un attento “filologo dei simboli”; la
sua opera costituisce per noi una rarissima testimonianza della concordanza,
caduta poi in seguito nel dimenticatoio, per la mancanza di una continuità di
rappresentanza reale e non solo apparente dei vertici in verità di entrambe le
parti in causa, tra ermetismo e dottrina cattolica romana. René
era il nome che l’autore prese entrando come novizio nella congregazione dei
Fratelli di San Gabriele e di cui fece parte fino al suo scioglimento nel 1903. L’autore
ci conduce per mano nella rappresentazione che gli antichi egizi si
tramandavano del cuore umano inteso come una realtà a se stante, diremmo
volentieri come Uomo interiore, sede privilegiata delle facoltà intellettuali e
non solo delle passioni. Il
sacerdote egizio contemplava nel suo cuore la Legge della Unità della
Creazione, il Cuore eterno palpitante dell’unico Dio. Questo
ci fa riflettere, non poco, sul valore non solo sentimentale o devozionale che
in principio doveva avere il culto cattolico del Sacro Cuore del Cristo. Per
gli egizi, popolo di religiosi e non di creduloni come qualcuno oggi ci
vorrebbe far credere, il cuore umano, aveva come simbolo geroglifico il Vaso ed
era ritenuto il crogiuolo nel quale la volontà umana individuata assisteva al
nascere delle passioni terrene, governandole per il proprio bene; ed è per
questo che essi credevano che dipendesse dalla sua testimonianza, del cuore
appunto, resa dopo la morte fisica dal suo peso, la conservazione o la
distruzione dell’anima individuale nel giudizio.“Tribuat tibi secundum cor
tuum”.
Antimonio Un
fratello di Hermes SIMBOLI DEL CUORE DI CRISTO di Rene’ Louis Charbonneau-Lassay Ed. Arkeios Roma 2003 pag..15-25 Il cuore umano e la nozione di Cuore di Dio nell’antico Egitto Per un numero ancora troppo elevato di
cattolici, la pietà verso il Cuore Divino è una concezione tarda, nata nel
secolo XVIII dalla spiritualità sentimentale diffusa dai gesuiti e da altri
predicatori. Per altri — fra quelli che si sentono obbligati a riconoscere che
la fede del Medio Evo, soprattutto, ha onorato e adorato come noi il Cuore
redentore — questa è una idea germogliata nello spirito così devoto di quella
società medievale tutta impregnata di tenera poesia, ma al tempo stesso di un
realismo sorprendente. Si potrebbe quasi arrivare a dire che il culto del
Cuore, centro di tutto l’amore salvifico, deriva dalle «Corti d'Amore» e dalle
meditazioni infiammate delle monache. In ogni caso, viene ammesso, quasi come
scienza certa, che l'animo cristiano del primo millennio non ha avuto né ha
potuto avere nemmeno l'ombra di un pensiero per il Cuore di carne di Gesù,
fulcro dei suoi sentimenti affettivi, e che questa concezione si colloca
totalmente al di fuori del suo ambito. A maggior ragione, sembrerà loro
assolutamente stupefacente che l'intera casta sacerdotale di un popolo pagano
tra le prime civiltà umane abbia avuto per il Cuore del Dio unico — superiore
ai suoi dei, per quanto potesse concepirlo — una idea, una attenzione così
particolari, da fare attribuire al Cuore tutto ciò che la Divinità stessa
possiede di perfezione: potenza creatrice, scienza, bellezza, bontà e giustizia
infinite, e che questa idea, questo Sacerdozio abbia coinvolto tutta la nazione
con i suoi superbi sovrani, i suoi artisti, i suoi studiosi ed i suoi
architetti incredibili. Tuttavia, le scoperte fatte soprattutto
negli ultimi vent’anni dall’egittologia, permettono di affermare, su una base
di documenti materiali positivi (scritti, iscrizioni lapidarie, sculture,
oggetti d’arte, ecc.), cose la cui mirabile testimonianza è indiscutibile. Sin dal tempo delle prime dinastie
storiche, dal 3300 al 2600 a.C., l’Egitto ci si mostra attraverso i monumenti
come una nazione estremamente civilizzata; le statue e le sculture che abbiamo
di quel tempo sono di un’arte la cui perfezione ci confonde, e quando i Faraoni
della quarta dinastia, Cheope, Chefren e Micerino, elevarono o permisero ai
Sacerdoti di elevare quei misteriosi santuari che sono le Grandi Piramidi di
Giza fra il 2840 e il 2680 prima della nostra era, la scienza degli egizi nei
campi dell'astronomia, cosmogonia, geometria e geodesia era tale che ci sono
voluti i nostri attuali strumenti di precisione per eguagliarla; e i loro
metodi matematici nel campo delle suddette scienze hanno permesso loro di
risolvere calcoli tali da lasciare stupefatti i nostri scienziati. Ora, prima ancora di quell’epoca, quando i
pontefici di Men? e di Tebe erano i custodi della scienza e della religione in
Egitto, vi si conservava anche il culto del vero Dio — a onor del vero
alterato, ma espressamente indicato per esempio dai geroglifici dei monumenti
della terza e quarta dinastia — il Dio Uno, Unico. Entità spirituale, appariva
come completamente diverso dagli dèi, che non furono altro che totem, o dagli
antenati divinizzati, a cominciare da Atum (l'Antenato); uno dei suoi ?gli,
Osiride, divenne uno dei ministri della Divinità unica incaricato specialmente
di presiedere alla pesa delle anime sulla soglia del «regno delle
trasformazioni». Quanto al Dio unico di cui parla il pagano
egizio che in quel tempo scrisse il papiro del British Museum, leggiamo la
seguente espressione: «Dio grande, Signore del cielo e della terra, che hai
fatto tutte le cose esistenti. O mio Dio, mio Maestro, che mi hai fatto e
formato, dammi un occhio per vedere, un orecchio per udire le tue glorie!»,
preghiera che ritroviamo simile nei Classici di Roma e dell’antica Grecia. Ciò che spicca fin dal primo contatto che
si ha con le opere specialistiche che trattano delle ultime scoperte religiose
dell’egittologia è che il popolo egizio custodì a lungo la nozione di verità
primarie e che, d'altra parte, sebbene non fosse «la nazione in cui tutte le
nazioni sono state benedette», in tale popolo, e soprattutto nella sua casta
sacerdotale e nella sua élite intellettuale, vi dovettero essere animi molto
nobili, spiritualmente molto puri, che Dio favorì di illuminazioni e intuizioni
meravigliose. Non dobbiamo stupirci: il Melchise- dech di cui parla il Genesi e
i tre Magi dei Vangeli non erano affatto ebrei, eppure il primo prefigurò
l'eucaristia e i secondi scoprirono Cristo appena nato: «Lo spirito di Dio
soffia dove vuole». E per questo che troviamo nei testi sacri
dell'Egitto dei brani davanti cui grandi studiosi di oggi come Alexandre Moret,
professore al Collegio di Francia e Direttore della Ecole Pratique des Hautes
Etudes, non esitano a vedere una sorta di «precristianesimo»; così Moret, nel
suo magnifico studio Mystères Egyptiens titola arditamente uno dei suoi più bei
capitoli « Le Mystère du Verbe Créateur». Sono i resti di queste antiche credenze
dei bei tempi dello splendore egizio che, raccolti nei Libri Ermetici,
stupivano a tale punto i nostri primi dottori cristiani che uno di loro,
Lattanzio (T 325), diceva: «Ermete ha scoperto, non so come, tutta la verità». Vediamo ora, stando ai documenti più
antichi, quale posto sorprendente viene dato al cuore umano nella concezione
della psicologia religiosa che non era ancora stata penetrata, se non di poco,
dal politeismo e dalla zoolatria degli ultimi secoli della decadenza egizia.Nei
gerogli?ci, scrittura sacra o spesso immagine della cosa che rappresenta la
parola stessa che indica, il cuore non fu tuttavia raffigurato che da un
emblema: il vaso. Il cuore dell’uomo non è in effetti il vaso in cui la vita
viene rigenerata continuamente dal suo sangue? Il vaso in cui nascono, si
sviluppano e muoiono le passioni buone o cattive che presiedono alla sua
volontà e che talvolta la dominano, al punto da tiranneggiarla a loro
piacimento.Alla nascita del genere umano, come racconta a suo modo la piramide
del Faraone Pepi II, Atum, il primo uomo genera i suoi figli suddividendo il
suo cuore in nove parti, e ciascuna di esse diviene un essere umano completo;
così nacquero gli antichi dei e dee Turn, Shu, Tefnut, Keb, Nut, Osiride,
Iside, Seth e Nefti. Questo per far comprendere che l'uomo trasmette la vita
per mezzo del suo cuore, come vedremo più avanti il Verbo di Dio creare la vita
con il suo Cuore.
Fig. 1. Il vaso,
emblema geroglifico della parola «cuore». Dal cuore proviene tutto ciò che l’uomo sa
e può fare; è ad esso che l'attività umana chiede la sua ispirazione; è quello
che ci rivela quel Faraone prestigioso del secolo XV a.C., Tutankhamon, che ci
è stato restituito nello stupefacente splendore dei suoi tesori funerari. Il
testo che ci parla di lui, sulla stele, assicura testualmente che «meditava
profondamente sulla felicita‘ del popolo comunicando con il suo cuore». E quando Ramses II rimprovera ai suoi
ufficiali di essere stato male assistito nel corso di una battaglia, dice loro:
«Non vi porto più nel mio cuore»; poi, rivolgendosi verso suo padre che è in
cielo, il Dio Ammone, osa parlargli così: «Che fai tu dunque, padre Ammone? Non
è compito di un padre vegliare sul proprio figlio [...]. E cosa sono per il tuo
Cuore questi asiatici ?» °. E dunque proprio del Cuore di Dio, del Dio
Ammone (1), che si tratta, ma soltanto, e ciò è molto chiaro, del Cuore
metaforico di Dio in quanto centro degli affetti divini; forse che alcuni dei
nostri testi di liturgia cattolica non lo supplicano con accenti talvolta
simili? Oh! Il cuore umano, quanto lo ha amato
l’Egitto idealista! Si legga la favola poetica di Bitau, anch’esso
sacrificatosi, ma il cui cuore non vuole morire e si trasforma ogni volta che
un nuovo colpo, di per se stesso mortale, lo colpisce; fino a quando Anubi
rianima Bitau ritrovando il suo cuore errante e mettendolo nell'acqua. E Bitau
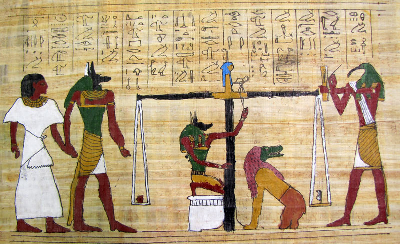
ritorna in vita con il suo cuore. Ma è soprattutto nel giudizio delle anime,
nella dipartita dalla vita terrena, che il cuore appare come il riassunto
completo dell'uomo. Questa pesatura degli atti delittuosi di ogni umana
esistenza è espressa dalle scene scolpite sui monumenti dell’antico Egitto,
tutto sommato abbastanza simili a quelle che ci mostrano sulle nostre chiese
romaniche e gotiche il giudizio particolare delle azioni della nostra vita, con
san Michele che pesa delle anime minuscole in presenza dell’angelo custode che
ci protegge e di Satana nostro accusatore.
Fig. 2. Libro dei
morti. Papiro. Museo egizio di Torino. Cosa ci mostra la scultura egizia? Davanti
al trono di Osiride, incaricato del giudizio dei Morti e circondato dai suoi
consiglieri, si erge una bilancia vicino a Maat, personificazione divina della
Verità; a fianco o sopra di essa, un mostro ibrido, il Divoratore, giustiziere
della divinità, è pronto a impadronirsi dell'anima se la giusta pesatura
andasse a sfavore di questa. Su uno dei piatti sta solo il cuore del
defunto, con le sembianze del vaso gerogli?co in cui stanno le opere malvagie
della vita che sta per essere giudicata. Allora Maat—Verità avanza, stacca
dalla sua acconciatura la piuma bianca di struzzo che la caratterizza, talvolta
si siede lei stessa sul piatto, però, siccome è sostanza spirituale, l'unica
cosa che pesa e‘ la piuma bianca... E se l’equilibrio perfetto non viene a
crearsi subito fra il vaso-cuore e la piuma immacolata, è il mostro giustiziere
che trionfa, e l’anima non verra‘ ricevuta nel regno delle trasformazioni
felici. Vedete: sulla pietra della sua tomba c’e‘
Ramses VI che la bella dea-antenata Iside, figlia di Atum, conduce per mano
davanti al tribunale terribile di suo fratello Osiride con i suoi consiglieri,
davanti alla incorruttibile Maat-Verità; il Faraone recita il suo «mea non
culpa», poiché solo il male commesso entra in gioco. E Ramses comincia: Omaggio a Te, Dio grande che possiedi la
certezza! lo vengo a te, o mio Signore, mi presento al tuo cospetto per
contemplare la tua gloria. Io ti conosco, conosco il tuo Nome e conosco il nome
delle quarantadue divinità che sono con te nella sala della Verità. Non ho
messo l’iniquità al posto della dirittura. Non ho fatto quello che gli dei
detestano. Non ho ucciso ne' fatto uccidere perfidamente. Non ho tradito
nessuno. Non ho fatto versare le lacrime dei poveri, ecc. Quarantatré capi d’accusa sono così
rigettati dal Faraone che conclude gridando: Sono puro, sono puro, sono puro! E mentre la Verità lo guarda e si appresta
a lasciar cadere nel piatto della bilancia la sua piuma terribilmente leggera,
lo scarabeo di pietra preziosa, che occupa nella mummia regale il centro del
cuore, ripete per invocazione la frase magica che fu detta su di lui quando fu
consacrato dagli ieroduh': O cuore, che eri il mio cuore sulla terra,
tu che provieni da mia madre e mi sei necessario per le mie trasformazioni, non
testimoniare contro di me, non opprimere tuo padre, o mio cuore! Ma appena Maat—Verità ha lasciato cadere
la piuma del suo diadema, i due piatti della bilancia oscillano e si fermano al
punto preciso dell’equilibrio perfetto, Ramses è giustificato. Sulla sua stele funeraria conservata al
Museo di Torino e tradotta da Chabas, Beka, prima di recitare come Ramses il
suo «mea non culpa», lo riassume in anticipo, con queste parole vincitrici: «lo
fui un uomo giusto, sincero e buono, che ha messo Dio nel suo cuore» ".
Dio — Beka dice proprio Dio — in geroglifico Nuter", e non uno degli dèi.
Beka comprendeva al meglio che non poteva essere condannato un cuore in cui
risiedeva Dio e che viveva di Lui, poiché lo possedeva al centro stesso della
sua vita! Dopo di lui, e quasi nello stesso senso,
il Cantico dei Cantici farà dire all'anima: «Pone me ut signaculum super cor
tuum», «O Dio, mettimi come sigillo sul tuo cuore». Ben mille anni dopo
un’altra frase, ancora più espressiva, quella di san Paolo, le farà da eco:
«Non sono più io che vivo, ma è Cristo che vive in me». Dunque, per l’Egitto religioso il cuore
era tutto l'uomo: la sede delle sue facolta‘ intellettuali, come anche delle
passioni che con esse governano la sua volontà, il vaso di vita dove l'anima,
abbandonando il corpo, lasciava il deposito delle azioni compiute con esso, il
tabernacolo infine dove il giusto portava la Divinità quando per mezzo delle
virtù aveva serbato Dio in lui, come Beka che se ne gloriava. L'attenzione del pensiero egizio era
troppo rivolta al cuore umano e, oltre al suo ruolo fisico, gli attribuiva una
parte troppo importante perché essa non risalisse, forzatamente, verso il cuore
di quella Divinità unica che la casta sacerdotale di quel paese riconosceva
come posseditrice di onnipotenza e di ogni perfezione, fino al sommo grado della
totalità e dell'infinitezza. Sono il Faraone Amenofi IV, detto Ekhnaton
— il cui magnifico e elegante busto si trova al Louvre — e la regina
Nefer—Neferiu—Aton, sua sposa, che composero insieme gli splendidi cantici che
monumenti vari ancora intatti ci hanno conservato. In uno di questi inni,
rivolto a Dio, al Dio-Aton, vale a dire considerato sotto l'emblema radioso del
disco solare, leggiamo a caso da un lungo testo frasi come queste: Tu hai creato la Terra nel tuo Cuore,
quando eri tutto solo [...] hai fatto le stagioni dell'anno per far nascere e
crescere tutto ciò che hai creato […] hai fatto il Cielo lontano per levarti in
lui e vedi da lassù tutto ciò che hai creato, tu, tutto solo [...] Appari sotto
le sembianze di Aton vivente, ti levi radioso, ti allontani e ritorni; tu sei
nel mio cuore “°. Quindi, stando all’inno di
Amenofi-Ekhnaton, è dal Cuore stesso di Dio che è partito il gesto divino della
grande azione creatrice: «Tu hai creato la Terra nel tuo Cuore». La stessa assicurazione ci viene data
anche dall'iscrizione funebre di un sacerdote di Menfi il cui testo e senso
sono stati precisati da Breasted, Maspero ed Erman; ne deriva che i teologi
della Scuola di Men? distinguevano nell’opera del Dio Creatore il ruolo
dell’idea creatrice che essi chiamano la parte del Cuore, e quello dello
strumento della creazione, che essi chiamano la parte della Lingua. Dunque, in
Dio ogni Verbo è un concetto del Cuore, e per attuarsi ha bisogno della parola;
così si forma ogni atto divino nell'idea del Cuore, nell’emissione della
lingua. Quindi, il Cuore di Dio viene visto dai
saggi dell'Egitto non soltanto come fulcro iniziale della potenza creatrice ma
anche come la sede del pensiero divino, ed è per suo mezzo che Dio possiede la
scienza infinita di tutte le cose. Sul papiro di Leida, a proposito di Dio
indicato con il nome di Ammone, si legge: «Il suo Cuore conosceva tutto, le sue
labbra gustavano tutto». Un'altra Scuola teologica che ci fa
conoscere alcuni monumenti dell’epoca dei Ramessidi (XIX dinastia, circa 1250
a.C.) ci espone un’altra teoria teologica secondo la quale Dio — il Dio unico
(lett.: il Nome) la cui natura è tutta mistero — ci viene presentato composto
da tre entità divine che formano una autentica trinità—unita‘: Ptah, Horo e
Thot. Ptah è la persona suprema e rappresenta l’Intelligenza divina; Horo,
secondo una tradizione antica già all'epoca, ne è il Cuore; Thot è il Verbo,
strumento delle opere divine. E Ptah è quindi designato come l'Essere Supremo
perche' la triade intera procede in qualche modo da lui; questo seguendo lo
schema del precitato documento: «Colui che diventa Cuore, Colui che diventa
Lingua» ". La seconda persona di questa trinità,
Horo, il Cuore divino, nell'emblematica sacra fu rappresentata sotto le
sembianze dello sparviero, del falco. Sin dai tempi della IV dinastia, cioè
circa tremila anni prima della nostra era, si trovava sulla bandiera sovrana
del Faraone Chefren la doppia corona degli Egizi del Nord e del Sud, e nella
formula geroglifica del suo nome appariva il Vaso-Cuore. Il falco-re, il falco-dio fu il totem,
cioè il genio e il simbolo abituale dei Faraoni considerati sia come figli che
come emanazioni terrene della Divinità, come fu anche l'emblema di Horo, il
Cuore di Dio. Sulla bella statua dello stesso Chefren, lo sparviero sacro
poggia il suo cuore contro la nuca del Faraone che protegge, racchiudendo la
sua testa nelle ali spiegate. Mi domando se questa posa non indichi
molto più di una semplice protezione... Essa è certamente espressiva, dato che
l'uccello divino copre con il suo cuore il cervelletto del sovrano nel punto
più sensibile, a livello del «ponte di Varolio», e che il suo corpo protegge
fasci di nervi cervicali che alcuni anatomisti chiamano «albero della vita».“
ma non vi sarà dell'altro? Molte sono le sculture sacre d’Egitto che
ci mostrano dei sacerdoti, degli oranti o altri operatori che fanno imposizioni
magnetiche su un soggetto; a volte una intera assemblea le indirizza verso un
personaggio altolocato, per esempio un Faraone che nasce, e un testo uf?ciale
ci dice della Faraona regnante Hatshepsut che « gli dèi lanciano costantemente
i loro ?uidi di vita su di lei ogni giorno» “.
Fig. 3. Statua di
Chefren, Museo del Cairo. Non potrebbe trattarsi, nel contatto così
suggestivo che li unisce, di una sorta di comunicazione, di trasmissione di
questa natura, di una maniera di comunicazione mediante emanazione e
assorbimento dei caldi fluidi divini fra il cuore dell'Uccello-dio e il
cervello del Faraone Chefren?… Circa mille anni dopo di lui, quando sul
suo trono, il più grande dei troni, lo sfarzoso Tutankhamon risiedeva in tutto
lo splendore della sua magnificenza, anche le sue braccia riposavano così,
nude, fra le ali spiegate del grande sparviero di lapislazzuli... E presso gli
Egizi come presso gli Ebrei, era alle braccia che si riferiva l'idea della
potenza, dell'autorità. Non voglio affatto esagerare, ne’ essere
così sistematico al punto di affermare che la teologia talvolta così strana
dell’antico Egitto abbia contenuto, se così si può dire, una preistoria del
nostro culto cattolico al Cuore divino: certo no; ma ho ritenuto che fosse cosa
buona per lo meno esporre in questa sede quale grande parte ha avuto nel suo
pensiero, e quale posto e quale ruolo ha saputo riconoscere al Cuore del Dio
onnipotente, onnisciente e buono, la religione di questo popolo pagano;
religione grossolana e materialista per certi versi, quasi spoglia di
ascetismo, ma così elevata per certi dogmi e così eloquentemente espressiva per
le sue formule di adorazione e di preghiera. Oso pensare che, se i nostri santi dottori
dei secoli medievali avessero conosciuto i dati che le scoperte di questi
ultimi tempi hanno rivelato sulle idee e le cose dell’antico Egitto, con tutta
probabilità oggi ne troveremmo delle tracce nella patristica del Sacro Cuore, e
forse addirittura nella liturgia: il rituale romano ammette proprio nell’ufficio
dei Morti la testimonianza degli oracoli sibillini in accordo con quelli del re
profeta: «Teste David cum Sibylla». Sicuramente non è da mettere in parallelo
il Cuore fisico di Gesù che fu adorato in primo luogo come la principale delle
ferite redentrici e come fonte corporea del Sangue salvifico, con il Cuore
puramente metaforico al quale gli egizi guardavano come fonte di bellezza?
delle perfezioni divine; ma resta il fatto che il cuore, fosse quello di Dio o
quello umano, metaforico o corporeo, essi lo rappresentavano separatamente dal
resto della forma umana, con un comune emblema consacrato, il vaso gerogli?co,
dal simbolismo assai parlante. Nessun altro popolo antico attraverso il Cuore
guardò la Divinità, nessuno mai le si rivolse scongiurandola di avere pietà di
lui, come scongiurava il proprio cuore di non testimoniargli contro nell’ora
suprema. Proprio i testi gerogli?ci ci lasciano
intendere che tale attenzione dell’anima egizia verso i Cuori di Dio e
dell’uomo non corrispondeva per nulla a uno stato spirituale particolarmente
sentimentale. Per quello che ci interessa, l'elite religiosa dell’Egitto, per
quanto deviata sia stata nella teologia generale, ci appare troppo scientifica,
troppo speculativa, per essersi lasciata tentare più dalla dolcezza del
sentimento che da ri?essioni serie e ragionate.
Note Signore di ciò che è, permanente in tutte
le cose, Unico in sua natura come il Seme degli dei
[…] capo di tutti gli dei.[…] La tua dolcezza è nel cielo
settentrionale, la tua bellezza rapisce i cuori, l'amore
di te fa languide le braccia, la tua forma bella rende deboli le mani, e
i cuori, alla tua vista, ogni cosa dimenticano. Tu sei l'unico che fece tutto ciò che è.»
(Inno ad Amon-Ra, Papiro Boulaq) |
