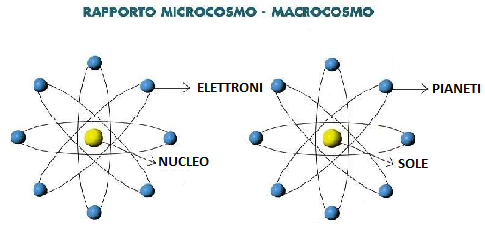
MACROCOSMO E MICROCOSMO L'origine di questi termini filosofici è, essenzialmente, platonico-aristotelica: Platone chiama il mondo «grande uomo» e Aristotele contrappone il «grande mondo» al «piccolo mondo». Naturalmente, dei due termini riferentisi al concetto di cosmo, originario è quello di "microcosmo", esprimente l'idea dell'uomo come in sé organizzato in forma analoga a quella dell'universo, e quindi esso stesso "piccolo universo": e la definizione dell'«uomo» come «piccolo mondo» sembra sia stata data per la prima volta da Democrito. Contrapposto all'uomo come "microcosmo", il mondo reale doveva assumere di conseguenza il nome di "macrocosmo". I filosofi
greci Anassimene di Mileto, Pitagora, Eraclito e Platone,
gli antichi gnostici, Filone giudeo e il filosofo medievale ebreo
Maimonide, abbracciarono tutti l'idea del macrocosmo-microcosmo.
I Sufi del XII° secolo dicevano che il macrocosmo è il
microcosmo, una sorta di versione antica dell'idea di Blake di
vedere il mondo in un granello di sabbia. Ermete Trismegisto
disse che una delle chiavi principali per la conoscenza era la comprensione che
“l'esteriore è come l'interiore delle cose; il piccolo è come il grande”. Gli alchimisti
medievali distillarono questo pensiero nel motto: “come sopra, così
sotto”. Il Kremmerz così si esprimeva: “Macrocosmo e microcosmo, in ambito ermetico ed esoterico, designano due entità di cui l'una è riproduzione in scala dell'altra, e che per via della loro
somiglianza formano un insieme indivisibile, un'unità dove le parti (il
microcosmo) sono in rapporto al tutto (il macrocosmo)”. Da quanto
precede risulta evidente che la chiave interpretativa dei rapporti esistenti
tra Macrocosmo e Microcosmo è l'”analogia”. Sinteticamente
e semplicemente, possiamo intendere l'analogia come “il rapporto
che la mente coglie fra due o più cose che hanno nella loro costituzione, nel
loro comportamento o nei loro processi qualche tratto comune”. Il Kremmerz
a tale proposito insegna: “Tutto è
analogico, e il processo magico per eccellenza è l'analogia”. Poi, per spegnere gli eventuali facili entusiasmi dei novizi, precisa: “L'analogia
è il terribile scoglio del novizio alla iniziatura, in quanto egli non la
discopre che col progredire della sua purificazione”.
Ermete Trismegisto, nella seconda proposizione della sua Tavola di Smeraldo ha iscritto: «Ciò ch'è in basso è
come ciò ch'è in alto, e ciò ch'è in alto è
come ciò ch'è in basso, per fare i miracoli della cosa una. E poiché tutte le realtà sono e provengono da una, per la mediazione di una, così tutte le realtà sono nate da questa realtà unica mediante adattamento.» L'universo è il macrocosmo e l'uomo è
il microcosmo. Similmente l'uomo rappresenta il macrocosmo dell'atomo (sistema solare in piccolo). L'uomo è il macrocosmo del microcosmo, egli riflette
l'universo, è il grande simbolo dell'universo.
Ciò ci conferma il postulato della saggezza antica: “Tutto ciò che esiste nell'Universo è
fatto ad immagine di Dio”. Siamo un frammento del divino, una sua scintilla.
L'essere unitario immenso è globale, l'Universo grande è il pieno, il riempito, il gonfio. Etereo o pesante è compresso di materia, superbamente evaporante e determinante correnti di sottili, intelligentissime forme e forze, moto, vibrazione, armonia, ove ogni spostamento di molecole planetarie e stellari ha un riflesso e una reazione sui limiti infinitamente lontani del grande corpo. Il Kremmerz diceva: “L'Universo è la sintesi
di un'unità immensa, incommensurabile ed è uguale – per analogia – a qualunque
unità organizzata di un ordine inferiore. Il corpo umano è un esempio. Ora
mettendo in relazione le due unità macrocosmo e microcosmo, cioè l'universo e
l'uomo, è logico, è strettamente scientifico, per quanto non sia sempre
sensibile, che qualunque movimento di una parte del creato influisce
sull'altra e ne modifica le condizioni “. La nostra Terra, immersa nell'oceano cosmico, ha legami invisibili con il mondo stellare che sovrasta, come una cupola, la nostra sfera. “Tutto è Uno”. Le attuali scoperte della fisica matematica, applicata alla
Cosmologia (Fred Hoyle, Pietro Banna, Giuseppe Arcidiacono) hanno dimostrato
l'esistenza d'un principio d'interscambio, per il quale ogni
particella (materiale o vivente) dell'universo è in continuo e reciproco
rapporto con il tutto. Perciò nel Cosmo (quindi anche nella nostra
galassia e nel nostro sistema planetario) tutte le cose sono legate tra
loro da azioni o influenze reciproche, influenze di cui la scienza ancora
ignora l'esatta natura (Andrea Saetti – Tratto da Cecco d'Ascoli, un poeta
occultista medievale).
L'ologramma ci conferma concretamente che nell'Uno,
governato dalla Legge Unica, la parte è simile al Tutto e che l'analogia è lo
strumento che permetterà all'uomo di integrarsi coscientemente con Esso. Il termine “ologramma” deriva dal greco òlos, intero, e gramma, scrittura: registrazione completa. L'ologramma si ottiene tramite una particolare tecnica
ottica chiamata olografia che, avvalendosi di sorgenti luminose
coerenti (laser), consente sia la registrazione fotografica tridimensionale di
un oggetto su un'unica lastra, sia la successiva ricostruzione, sempre
tridimensionale, dell'oggetto stesso. Con questa tecnica è infatti possibile
registrare su una lastra fotografica il campo completo della luce diffusa
dall'oggetto in osservazione (ologramma) per poi ricostruirlo con
tutte le sue peculiarità: osservando il campo ricostruito non si è in grado di
distinguerlo da quello naturale, e pertanto si vede un'immagine spaziale
dell'oggetto assolutamente simile all'originale.
Lo studioso attento, facendo le dovute analogie tra sorgenti luminose ed aura, lastra ed astrale, immagine simile all'originale e “doppio”, potrebbe sviluppare interessantissimi concetti da sempre tramandati dalla Scienza Sacra. L'olografia ci insegna che la lastra fotografica su cui sia
impressa un'immagine olografica possiede delle proprietà straordinarie. Se
frantumiamo con un martello la lastra, ne prendiamo un frammento e lo
osserviamo con attenzione: scopriamo, allora, che il frammento continua a
riprodurre l'intera immagine. Se prendiamo un altro frammento, troviamo anche
in esso che l'immagine è riprodotta nella sua interezza. Lo stesso vale per
tutti gli altri frammenti. - Ologramma: il frammento riproduce l'intera immagine.... La scienza ci ha così offerto un magnifico esempio a conferma della massima tramandataci dalla Saggezza Perenne: “Tutto è Uno” . Questa straordinaria proprietà dell'ologramma mi riporta alla mente un concetto della numerologia esoterica espresso dal Kremmerz: “Se 1 è sintesi, principio attivo, universo immenso (il macrocosmo), il 2 è il principio passivo della sintesi. Ogni unità che si immagina divisa in parti, cessa di essere tale. Quelle parti in cui l'erudizione elementare (non pitagorica) delle scienze occulte ci vuol divisi corpo, perispirito e anima o spirito, non sono divisioni ma componenti organici essenziali. Ossigeno e idrogeno non sono acqua, ma combinati lo sono; l'acqua divisa nei suoi componenti non è più tale. Non è dunque possibile la concezione di parti nell'unità. Qualunque divisione di un'unità sintesi in cui le varie parti sono compenetrate, fino alla monade, contiene i 3 fattori senza separarli mai”. Concludo con quanto insegna la Magia sulla costituzione dell'uomo e tramandataci dal Kremmerz: “L'uomo deve essere considerato come
un Essere, che contiene in sé i 4 elementi che costituiscono l'universo: 1° – Terra – Corpo Saturniano - Mangia, divora, si rinnova, si riproduce; 2° – Acqua – Corpo Lunare - Vive della fonte del primo come la Luna dalla luce del Sole; 3° – Aria – Corpo Mercuriale - Individualità risultante, cioè uomo mentale, alato al capo e ai piedi e il più in contatto con Giove, IO Superiore; 4° – Fuoco – Corpo Solare - L'individualità divina, la quale non si manifesta all'uomo che per mezzo del corpo mercuriale, che a sua volta si manifesta al lunare e questo al saturniano. Il novizio deve comprendere che questa divisione è puramente
fatta per intenderci in maniera concreta ma non esiste veramente nell'uomo,
perché questi 4 corpi sono compenetrati in modo che ogni cellula, ogni
atomo del corpo fisico umano contiene gli altri 3 rudimentalmente o
atomicamente”.
La saggezza perenne ci tramanda che Tutto è Uno,
pertanto ne deduco che la suddetta affermazione possa applicarsi a due aspetti
del mondo “Uno”. Quali sono questi due aspetti? Uno corrisponde alla realtà della vita di tutti i giorni, oggettiva
ed esteriore, l'altro, invece, corrisponde alla nostra realtà intima, soggettiva
ed interiore. Il primo mondo è analogo allo stato di veglia
e quindi di coscienza, il secondo allo stato onirico, all'inconscio,
al Sé Superiore. La ricerca non deve spingerci all'evasione dalla vita
quotidiana per farci rifugiare in una vita tutta interiore, ma bensì deve
condurci all'equilibrio nell'integrazione armonica dei due mondi. Più vita, più significato, più coscienza … se realizzata
nell'armonia dei due estremi. Gli antichi saggi ci hanno tramandato
che questa coscienza, nell'uomo iniziato ai misteri della Scienza Perenne,
dovrà divenire vigile, attiva e realizzatrice, 24 ore su 24, il che sta ad
indicare che il suo stato di coscienza dovrà espandersi anche alla dimensione
onirica, nella quale egli dovrà operare e realizzare gli insegnamenti dei
Maestri.
Dua-Kheti |
SIMBOLISMO DEGLI ANIMALI SACRI DELL'ANTICO EGITTOIl Maestro Kremmerz
indicando al discepolo la via sicura da percorrere, come primo precetto gli
insegna a “credere nel Dio unico, armonia dell’universo visibile
e invisibile, Dio che è legge immutabile, che è verità e luce, che è giustizia
e bene, che è perfezione e misericordia”. Questo precetto è la colonna sonora del suo Inno al Sole “Unus,
pollentissimus omnium!” e del suo luminoso “Credo” nel
quale egli elenca le Virtù del settenario, cioè dei sette pianeti o come li
chiama lui “piani” ma subito dopo prosegue e conclude con: “Così credo” nell’Uno che tutto in sé contiene: Moto, Forma, Forza, Intelligenza, Bene, Amore e Morte. Credo
nell’ascenso dell’uomo all’UNO infinito, nella Legge Universa di
ciò che fu, che è, che in eterno sarà”. “Credendo” nel
precetto del Kremmerz, io ritengo che gli Dèi non siano che
aspetti diversi della manifestazione dell'Uno...che tutto in sé contiene. Dalle Acque della profanazione e del Lete, molti animali
furono messi in salvo nell'”Arca” del simbolismo Sacerdotale Egizio. Tebe o Tebha, infatti, significa Arca, ricettacolo di tutte
le matrici. La parola Arca, potrebbe etimologicamente derivare dal
sanscrito Ark che vuol dire Sacrificare e Sacrificio, cioè Sacrum-Facio, rendo
sacro, e trattandosi quindi di simbolismo sacro, in esso dobbiamo inoltrarci
come insegnavano i sacerdoti egizi: “con passo che non lascia impronta”. “Gli dèi non sono che manifestazioni dell'Essere Supremo” HORUS Animale simbolico: FALCO
- BAK o BIK
Falco, animale consacrato ad Horus. Horus è il principio di evoluzione superiore cui deve
aspirare l'umanità. Her è il nome di Horus e del suo volto e significa anche “SOPRA”. HER-BAK = “Testa di Falco” e “Volto di Horus”. E' anche il nome del “cecio” il cui aspetto ricorda il profilo del falco di Horus, in relazione al becco e alla curva caratteristica disegnata dalla regione dell'occhio. La sua vista non è per nulla abbagliata dal Sole! Il falco piomba sulla preda, l'afferra tra gli artigli, la spiuma in pieno
volo, e le trafigge il cuore bevendone il sangue.
Horus, che significa probabilmente "Il lontano", è una
divinità celeste egizia che ha la sua ipostasi nel falco. Horus è la forma latina del nome egizio Hr la cui lettura è Heru, è il dio del cielo di Edfu. Il mito di Horus Non esiste un solo mito di Horus ma cambia a seconda della civiltà e
del periodo: · Nei Testi delle piramidi troviamo il mito più arcaico su Horus, il quale ci racconta che egli nacque dal rapporto tra Osiride (ricostruito con un membro di legno, secondo altri sarebbe una candela, e non resuscitato poiché rimane in stato vegetativo e diventerà per questo il dio delle vegetazioni e della morte) con Iside che lo partorisce e lo nasconde. Diventato adulto, Horus affronta Seth con i suoi seguaci, detti "Seguaci di Seth", il quale gli strappa un occhio e viene rappresentato come un porco. Horus successivamente riprende l'occhio e gli strappa i testicoli, dona l'occhio a Osiride suo padre che si rianima e con questo completa il ciclo agrario. Una variante del mito è raccontata nella stele di Metternich: Iside nasconde Horus affidandolo alla dea Uto, ma uno scorpione inviato da Seth si introduce nel nascondiglio del bambino, lo punge e lo uccide. Iside, trovato il bambino morto, invoca Ra e ferma con un incantesimo la barca del Sole; ne discende il dio Thot, che infonde l'energia vitale di Ra in Horus, resuscitandolo.[1] · La versione ellenica invece ci è nota da Plutarco (45-125) come Mito di Iside ed Osiride: Seth con l'aiuto di alcuni compagni, fa costruire una cassa (o sarcofago) ricchissima che regalerà a chi si adatterà perfettamente, in realtà è un inganno per Osiride che appena entrato vi viene rinchiuso e gettato nel fiume Nilo. Però la cassa si incastra in un arbusto, per cui la moglie Iside può recuperare il corpo. Iside, si unisce con Osiride e concepisce Horus. Ma Seth scopre il cadavere di Osiride e lo smembra in quattordici parti disperdendole nel Nilo. Iside va quindi alla ricerca delle parti, le trova e le ricompone tutte tranne il membro, inghiottito da tre pesci e al cui posto ne metterà uno finto.[2] Osiride poi verrà imbalsamato, rivitalizzato e diventerà re degli inferi.[3] In riferimento a quanto sopra, vorrei aggiungere alcuni elementi utili ad interpretarne qualche analogia. Sempre secondo Plutarco, il regicidio
commesso da Seth uccidendo Osiride, tronca un regno durato 28 anni (28 è il numero delle fasi
lunari) e cade nel giorno del plenilunio. Questo periodo di tempo mi ricorda la
durata di 28 anni + 1 mese del 1° ciclo delle “Lunazioni”,
avute dal Kremmerz dall'”anonimo napoletano (Izar)”
e tramandate ai suoi discepoli. Infatti, nell'11^ Puntata del 1°
ciclo egli ci riporta: “Questa lunazione si chiamava Orakìa
ed era dedicata al dio Serapi di Tebe. Il culto di Serapi era lo stesso di quello di Horus e Serapi era un dio grandissimo della medicina, sanatore, ricreatore come Osiride.... Ma i Serapei o tempii di Serapide erano esclusivamente medici. Serapide era qualche cosa come Esculapio, Horus, Ermete, Kons. La forma divina della medicina era proprio di questo dio, i cui
responsi non si facevano mai aspettare”....In fine di queste notizie riporterò
alcune sagge risposte del grande Dio Serapide ai suoi consultanti – e il lettore ne farà profitto”. Al termine della Lunazione ci dona “Tre responsi di Serapide”. Leggendo la 13^ Puntata troviamo: “Questa lunazione è chiamata Ra-Muni
dal pontefice di Menfi dallo stesso nome o dal genio omonimo del
culto astartèo....In questa luna si invocavano i sette genii o potestà
astartei.... Nel 1° ciclo Izar ricorda un responso di Serapide, che in questa luna dette al poverello per 28 giorni come rimedio universale l'acqua di mare, le alghe del mare e dei fiumi, e il sale marino”. Da quanto sopra, si intuisce
facilmente che le “Lunazioni” sono una preziosissima miniera di
informazioni circa la tradizione caldeo-egizia. Inoltre, Iside è Myriam e pertanto sempre dell'influenza della Luna o Lunazioni stiamo parlando. Iside, ritrova la cassa con il corpo di Osiride, lo riporta in vita per una notte e
con lui concepisce Horus. Ma il corpo del re defunto è ritrovato
anche da Seth che ne fa scempio, smembrandolo in 14 pezzi. Le 14 parti del corpo smembrato rimandano ai giorni che intercorrono tra il plenilunio e il novilunio. Iside troverà e rimetterà insieme le parti e da “nera” , in 14 giorni, tornerà di nuovo “bianca o piena”. Poiché il Kremmerz, per
conoscere il significato profondo delle parole, consiglia di scavare sempre
nella miniera delle lingue cosiddette morte e nell'etimologia delle parole,
evidenzio che il termine Luna deriva dal latino l?na, da un più antico louksna, a sua volta dalla radice indoeuropea leuk- dal significato di "luce
riflessa"; luce di chi? Del “corpo di luce” del suo sposo Osiride naturalmente! Il culto di Horus è attestato dal periodo predinastico (3100 a.C.), grazie alla rappresentazione di un falco nella "Stele del re serpente Djet"[4], fino all'epoca romana quando il suo culto viene unito a quello della madre Iside.
In epoca predinastica si ebbero, con molta probabilità, diverse
divinità falco. La più importante delle quali era il dio-falco venerato nell'Alto Egitto. Quando i sovrani del Basso Egitto unificano le Due Terre, Horus assume il carattere di Unificatore dell'Alto e Basso
Egitto. Il sovrano egizio è considerato la personificazione di Horus, ossia l'Horo vivente; la prima tra le molte titolature che identificano un sovrano
dell'Egitto è il serekht ossia il nome-Horo caratterizzato appunto dal falco.  Nella mitologia egizia esistono
diverse forme di Horo. In alcuni miti, Horo è considerato figlio della
dea-vacca Hator, il cui nome significa letteralmente casa di Horo.
Il mito però maggiormente famoso è
quello che lo vuole figlio di Osiride ed Iside e vendicatore del padre nei confronti
di Setth, il quale gli tolse un occhio durante un violentissimo scontro. Durante il lungo periodo della civiltà egizia l'Horo di Ieracompoli assorbe, con un meccanismo di sinceritismo, svariate altre divinità locali aventi caratteristiche simili che
infine divennero aspetti diversi di una sola figura. Le forme sincretiche più comuni erano: Harakhti, Hornedjitef, Harsiesi, Harmakis, Haroeris, Harpocrates, Harsomtus e Hurum ma ve ne sono anche con gli dei solari Ra, Atum e Aton di cui la più conosciuta è quella di Ra-Harakhti. I figli di Horo sono quattro divinità
protettrici dei vasi canopi, i
contenitori delle viscere nel processo di mummificazione. Quattro genî egiziani, originariamente celesti, quindi funerarî,
raffigurati rispettivamente l'uno come uomo, gli altri come
personaggi con testa di cinocefalo, di sciacallo,
di falco. Il corpo è spesso rappresentato
mummiforme, e sono spesso raffigurati tutti insieme su un fiore di loto, dal
quale si dice siano nati. Sono loro che danno ai vasi canopi egiziani le tipiche
quattro teste, che ne costituiscono in epoca più recente il coperchio.
Presso i Greci e i Romani fu noto con il nome di Arpocrate e rappresentato come un bambino con un dito in bocca, gesto che indica un infante e interpretato come un invito al silenzio. Per coloro che avevano acquisito la dignità di entrare nel “Santo
Sanctorum” del “Tempio coperto” egizio invece, il gesto interpretato
come silenzio era solo un primo simbolo esteriore per il volgo che ne
racchiudeva uno più profondo e segreto.
Dall'etimologia del nome e dal suo aspetto di uccello, si deduce
che Horo fosse una divinità del cielo: i suoi occhi
simboleggiano luna e sole, il cui viaggio nel cielo è dovuto al volo di Horo.
Horus: nella mitologia egizia, dio del cielo, della luce e della bontà. Una delle principali divinità egizie, Horus era figlio di Iside, dea della natura, e Osiride, dio del mondo sotterraneo; quando Osiride fu ucciso dal suo malvagio fratello, Seth, dio dell'oscurità e del male, Horus vendicò la morte del padre uccidendo suo zio. Il dio Horus, figlio di Iside e Osiride, simboleggia l'energia medianica. E' il signore della
profezia, della musica, dell'arte e della bellezza. Horus era il dio dei cacciatori
ed era rappresentato da un falco. Successivamente fu identificato con il sole,
divenendo il simbolo della nobiltà, archetipo dei faraoni. Horus, il falco divino, divenne quindi il dio del
cielo, che aveva il sole come occhio destro e la luna come occhio
sinistro. La sua natura comprendeva una chiaroveggenza che gli
consentiva di vedere ogni cosa, una capacità visiva molto acuta e una
sviluppata consapevolezza. I quattro elementi naturali, terra, vento,
fuoco e acqua erano al suo comando. Horus, che rappresenta quindi l'equilibrio
del mondo naturale, è anche associato all'orizzonte orientale e alle
terre straniere. Il suo colore è il giallo.
In seguito all’uccisione di Osiride da parte di Seth, le dee Iside e Nefti vagarono sulla terra alla ricerca dei
resti del suo corpo smembrato, che Seth aveva sparso in varie parti dell’Egitto. Riassemblato il corpo di
Osiride, Iside utilizzò le sue arti magiche per resuscitarlo almeno
temporaneamente, così da potersi unire a lui e concepire un figlio. Fu allora
che Horus, l’erede vendicatore di Osiride e il legittimo successore al trono
d’Egitto, fu concepito. Molte leggende identificano Horus come un bambino nato segretamente a Khemmis e
tenuto nascosto in paludi di papiro. Iside, con tutta la sua magia ed astuzia, lo avrebbe nascosto e
protetto fino a quando non fosse stato abbastanza grande da sfidare suo zio Seth per la successione al trono.  La disputa per la sovranità tra Horus e Seth è una lunga e complessa situazione
che riflette l’importanza delle due divinità nella mitologia e nella cultura
dell’antico Egitto. Si dice che il dio del sole Ra sia stato il giudice che, presiedendo
al tribunale, divise in origine il territorio fra di essi: a Seth offri il dominio dell’Alto Egitto
mentre a Horus quello del Basso Egitto. Alcune fonti, però, narrano che Ra cambiò successivamente idea e non
favorì Horus in alcun modo. Ne seguì una contesa di otto anni durante la quale
Horus e Seth tentarono di superarsi l’un l’altro
in astuzia. In diverse occasioni sarà ancora la magia di Iside a proteggere Horus. Con il suo aiuto, Horus riuscirà anche a vanificare un
episodio di aggressione sessuale da parte dello zio, disonorandolo
pubblicamente nel corso del processo. Horus nel suo tentativo di essere
riconosciuto come legittimo pretendente al trono dell’Egitto unificato,
rappresenterà il diritto divino del faraone alla sovranità, e sarà una delle
divinità la cui influenza conferisce regalità e potere.
Durante la disputa fra Horus e Seth, quest’ultimo insegue il nipote nel
deserto e lo acceca cavandogli gli occhi dalle orbite. Horus è poi trovato da Hathor, in alcuni casi ritenuta sua madre
più di quanto non lo sia Iside. Sarà lei a restituirgli la vista sanandogli gli occhi con il
latte di gazzella. L’occhio lunare di Horus o udjat divenne una
potente immagine che simboleggiava la regalità, la forza, la purificazione e la
protezione. Per gli Egiziani l’udjat era un totem di protezione
che veniva frequentemente indossato come collana, collocato sulle fasciature
dei corpi mummificati e, in alcuni casi, dipinto sopra i feretri. Più tardi i
Greci, che furono fortemente influenzati dalla cultura egiziana, dipinsero il
simbolo di un occhio analogo sulla prua delle loro barche, affinché fosse di
buon auspicio per la navigazione. Ancora oggi, l’occhio di Horus ha una notevole influenza: le sue sembianze ricorrono, infatti,
nella gioielleria popolare, nell’arte e nel disegno. Molti ne sono attratti
senza conoscerne il significato, forse perché esso risveglia l’innato legame
con gli antichi egiziani e con i miti di Osiride.  Vorrei concludere questo scritto con una sintesi riportando
le parole che in La Porta Ermetica il Kremmerz
utilizza per spiegare il significato dei primi tre numeri e della
trinità o legge del tre.
“La legge del mondo è una, sempre
uguale e costante. Un principio attivo feconda un passivo
che nutrisce e accresce la forma embrionale del primo, poi la distacca e la fa
vivere di vita propria. L'uomo, la donna, il figlio. Il Sole, la Luna, la creazione. 1 (attivo), 2 (passivo) = 1 + 2 = 3
cioè attivo più passivo dà vita ad una forma che è la somma dei due. …..Osiride agisce su Iside, nasce Horus”. Dua-Kheti Note:
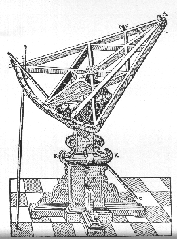
ASTRONOMIA AD OCCHIO NUDOIl cielo è il “soffitto” più alto. Osservandolo si ha la sensazione di una cupola semisferica. Da qualunque luogo si osservi si ha sempre la sensazione di trovarsi al centro. L’uomo ha investigato l’ambiente circostante mediante i propri sensi, in particolare mediante la vista. Il primo strumento ottico di cui l’uomo ha fatto uso per conoscere l’ambiente circostante (cielo compreso) è stato l’occhio, naturalmente nudo.
Un passo in avanti fu costituito dai Babilonesi che probabilmente utilizzavano mirini molto rudimentali ma che avevano costruito delle torri, gli ziqqurat, così da ridurre i disturbi ed avere dei riferimenti ad hoc, dalle quali effettuare le loro osservazioni. I sacerdoti mesopotamici arrivarono così a scoprire la periodicità delle eclissi lunari. Scoprirono che ogni 18 anni circa esse si ripetono alla stessa maniera. A testimonianza di quanto l’osservazione del cielo fosse accurata, un sacerdote, avvolto nell’aura del mito, rispondente al nome di Kidinnu, pare avesse calcolato il periodo sinodico della Luna con un errore di circa mezzo secondo. In ogni caso, fra alti ed inevitabili bassi, le mire sono andate via via perfezionandosi fino alla fine del XVI secolo. I migliori strumenti furono difatti quelli di Tycho Brahe, un astronomo danese (figure 2 e 3). Le sue posizioni, le più accurate, oltre a smontare buona parte delle concezioni aristoteliche, furono la base da cui partì Keplero per determinare le sue leggi del moto planetario di impostazione eliocentrica. I dati raccolti erano coerenti con gli algoritmi di Tolomeo, basati su una concezione geocentrica; tutti tranne tre. Keplero, per quanto in cuor suo convinto senza prove della bontà del modello copernicano, era così fiducioso nei dati di Tycho che per soli tre dati (su una mole vastissima) smantellò il millenario impianto geocentrico. Il tergiversare del boemo fra una forma di orbita ed un’altra fino al definitivo imporsi di orbite ellittiche di cui il Sole occupa uno dei fuochi fa parte dell’elaborazione a tavolino, non dell’osservazione diretta.
L’opera di Brahe fu però anche l’ultima conquista del cielo ad occhio nudo.
Nel 1609 Galileo Galilei ha sentore di un giocattolo inventato nelle Fiandre
(forse su idea di qualche occhialaio italiano) e comprende l’importanza che
l’oggetto può avere, opportunamente rivisto, per scopi scientifici. “La notizia
delle curiose esperienze fatte con questi occhiali arriva alle orecchie di
Galileo. D’ora in poi il decorso della storia del cannocchiale cambierà
radicalmente.” (V. Ronchi – “Il cannocchiale
di Galileo e la scienza del Seicento” –). Lo stesso Keplero sarà protagonista
di quella rivoluzione di cui l’artefice principale era stato Galileo,
realizzando un telescopio, chiamato appunto oggi kepleriano. Grazie agli
strumenti ingranditori la scienza astronomica può lanciarsi oltre gli orizzonti
del periodo precedente, andando ad investigare la natura dei corpi celesti, nel
solco di Galileo che aveva scoperto le montagne lunari, le macchie solari, la
(presunta) forma trilobata di Saturno, l’esistenza di molteplici centri di
rotazione con la scoperta di alcuni satelliti di Giove. A questa branca della
scienza astronomica si dà il nome di astrofisica, limitando l’ambito
dell’astronomia propriamente detta essenzialmente alla determinazione delle
leggi del moto.
Moto significa velocità, e la velocità è un rapporto fra due grandezze: lo
spazio ed il tempo. Anzitutto dunque, un laboratorio di astronomia necessita di
una definizione condivisa di questi due fondamentali parametri. Cominciamo dal
più complicato: il tempo. Il tempo è una variabile che scandisce il ritmo della
nostra attività e che entra nell’equazioni della fisica. Il punto essenziale è
l’esistenza nella mente umana di questa variabile suscitata da una realtà in
movimento (in un mondo statico nessuno avrebbe sentito la necessità di
introdurre questa variabile). Per Aristotele il tempo è una misura del moto in
base ad un prima ed un dopo. S. Agostino riconosceva le difficoltà di
definizione (“so che cos’è il tempo ma se me lo chiedi non so rispondere”).
Kant nella sua “Critica della Ragion Pura” lo definisce forma a priori della
sensibilità, assieme allo spazio, certo della sua fenomenica presenza dal
disporsi uno dopo l’altro dei sentimenti. I filosofi moderni, in sostanza non
hanno saputo superare il groviglio di problemi complessi che già i filosofi
greci avevano constatato (il più arguto fu forse Zenone che cercò di illustrarne
i problemi con una serie di esempi paradossali). Per loro fortuna la fisica e l’astronomia non necessitano di definizioni
apodittiche, si accontentano di definizioni operative che consentano di poter
maneggiare quelle grandezze, lasciando campo libero ai filosofi di trovare le
definizioni che si rivelano più adeguate. Accantonata dunque l’ipotesi di giungere ad una definizione univoca si
cerca una definizione operativa. Occorre misurare i cambiamenti del mondo in
cui viviamo, trovando un fenomeno ripetitivo che possa fissare una cadenza da
assumere come costante. Ogni fenomeno ciclico (che si ripete uguale a se stesso
più volte) può essere scelto per definire una scala di tempi. Dopodiché occorre
fissare nella scala, un’unità campione di riferimento ed un’origine, un punto
zero. Questo porta con sé alcune difficoltà: il tempo non si può maneggiare,
non si può spostare un intervallo di tempo per portarlo a confrontarsi con
l’unità campione (come si può invece fare con lo spazio); il fenomeno ripetitivo
scelto occorre che sia sempre presente o quanto meno attuabile. Quale fenomeno
scegliere? I battiti del polso? Le oscillazioni di un pendolo? Il fluire di
sabbia o acqua? Il consumo di una candela? Le posizioni degli astri (primo fra
tutti il Sole con l’alternarsi del giorno e della notte o delle stagioni)? Non
esiste scelta giusta o sbagliata ma solo scelta operativamente adeguata o
inadatta. Una volta eseguita la scelta, le osservazioni ed i controlli empirici
confrontati con le previsioni (basate sulle leggi fisiche) condurranno alle
opportune correzioni, o all’abbandono di un sistema per un altro migliore. Si
deve adottare la scelta più performante. La necessità di una scelta adeguata si
lega ad un aspetto non certo secondario: chi ci assicura che la periodicità sia
sempre rispettata? Purtroppo non esiste tale certezza, o se si preferisce, la
definizione operativa ci induce a rinunciare ad essa. Se ad esempio scegliessi come riferimento il battito del mio polso, il
mondo scorrerebbe più lentamente tutte le volte che ho la febbre. Se scegliessi
l’arco diurno del Sole, d’estate tutti i pendoli andrebbero più lenti che in
inverno, il polso correrebbe di meno, i fiumi avrebbero portata minore. Sarei
avvantaggiato per battere un primato di velocità! Inoltre cambiando località le
mie lancette dovrebbero correre più o meno velocemente! Tutte le leggi fisiche che coinvolgono il tempo dovrebbero predire questo
fenomeno e tenerne conto. Sarebbe una scelta operativamente adeguata? Dipende
dal contesto nel quale mi trovo. Le leggi fisiche che deduco in esso devono
però essere in grado di predire i fenomeni. Al proposito Einstein un giorno
portò un esempio. Se vedo un orologio su un campanile, devo essere in grado di
stabilire le leggi che lo regolano dall’osservazione esterna, l’unica che posso
fare. Possiamo aggiungere che fintanto che non entro dentro, pensare al
campanaio che gira una manovella o ad un ingranaggeria che muove
automaticamente le lancette sono due teorie alternative che possono entrambi
sopravvivere almeno finché non osservo un fenomeno che non ne escluda una. Se
l’orologio si ferma, è finita la carica o il campanaio si è stancato? Se vedo
il campanaio uscire e l’orologio che continua a marciare devo escludere la
prima, ma posso pensare di rivisitarla sostenendo che vi sono più campanai che
si danno i cambi. Il filosofo Popper sosteneva che la scienza è in grado solo
di stabilire la falsità di una legge, non l’assoluta certezza. Ma torniamo alle questioni astronomiche. Abbiamo da prendere in esame lo
spazio. Si tratta dell’altra forma a priori della sensibilità, secondo Kant.
Esso viene percepito mediante i sensi, in particolare con la vista ed il tatto,
come tridimensionale, a differenza del tempo monodimensionale. Varie sono le
rappresentazioni. In ogni caso per localizzare un punto occorrono tre
parametri: ad esempio altezza, larghezza, lunghezza, oppure altezza, azimut e
distanza. Ancora una volta sono più performanti tipologie diverse di
rappresentazione a seconda della forma di spazio che si vuole descrivere. Come per il tempo anche per le coordinate spaziali occorre una scala di
riferimento campione ed un’origine, un punto zero, in funzione del quale
esprimere la percezione dello spazio, la posizione. Abbiamo detto che il cielo
viene immaginato come una cupola sferica. Se il mio intento è quello di
occuparmi del cielo, in uno spazio a simmetria sferica, è performante un
sistema che tramite due coordinate identifichi l’orientamento (assoluto o
relativo) del punto ed un opportuno confronto di coordinate (con un altro punto
preso come origine) dia la distanza. La percezione del cambiamento di stato
delle cose è in sostanza la variazione dello stato spaziale (variazione
dei parametri di orientamento e distanza) nel fluire del tempo. Ad esso l’uomo
ha dato il nome di movimento, differenziando la variazione dello stato di moto
mediante la grandezza velocità, espressa come rapporto tra il vettore
variazione di posizione ed il tempo.
A quel moto che, a prescindere dalla velocità, presenta la caratteristica di
mantenere fissa la distanza da un riferimento si attribuisce il nome di
rotazione. Ed a prescindere dalla causa, la volta celeste e gli oggetti ivi
contenuti appaiono ruotare sopra di noi attorno ad un punto fisso (figura 4).
Detto questo, occorre stabilire un sistema di riferimento. Per il tempo, in
quanto monodimensionale, la questione si risolve più semplicemente. Lo spazio è
invece tridimensionale ed occorrono comunque tre parametri. Se però assumo che
il cielo, almeno apparentemente, sia semisferico a distanza costante, per
quanto sconosciuta dall’osservatore, disinteressandomi di essa posso
localizzare un punto sulla volta celeste mediante due soli parametri. La
sensazione che tutto il cielo sia una cupola in rotazione e che gli astri siano
incastonati su di essa fa capire come si debba aspettare la fine del ‘500 con
Digges e Bruno per far “esplodere” il cielo delle stelle fisse (figura 5).
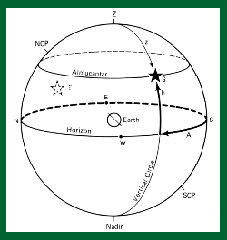
Poiché esiste una linea naturale detta orizzonte che separa la terra dal
cielo (che appare ruotare) il più semplice sistema (detto altoazimutale, figure
6) sfrutta queste due componenti: un piano che contiene l’orizzonte (il piano
orizzontale) ed un altro, univocamente determinato, ad esso perpendicolare,
passante per l’osservatore (in tutti i sistemi di riferimento l’osservatore è
il centro, l’origine delle coordinate spaziali), il fulcro della rotazione e lo
zenit (piano meridiano). Tali piani costituiscono l’origine di due angoli. Lo
scostamento angolare sul piano dell’orizzonte si definisce azimut, quello ad esso
perpendicolare altezza. Ad eccezione del mare aperto, dal punto di vista
operativo l’orizzonte si definisce male come piano, per la presenza di case,
alberi, muri. Viene pertanto definito come quel piano perpendicolare alla
direzione del filo a piombo.
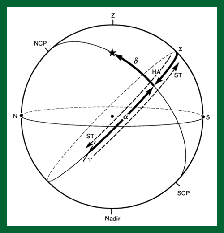
Il movimento dei corpi celesti lungo la volta suggerisce pure di utilizzare
un sistema legato agli stessi astri. Il sistema equatoriale relativo sfrutta lo
stesso piano meridiano dell’altoazimutale ed un piano contenente il cerchio
massimo della rotazione celeste (piano equatoriale). Rispetto ad essi le
coordinate vengono definite angolo orario (solitamente indicato con H)
e declinazione (abbreviata con d). Sostituendo il piano meridiano con un
piano passante per un punto “speciale” della volta e ad essa vincolato (e
quindi completamente svincolato dalla località dell’osservatore) si ha il
sistema equatoriale assoluto (figura 7), dove l’angolo orario viene sostituito
dall’ascensione retta (indicata con a). La differenza tra il sistema
equatoriale relativo e quello assoluto sussiste nella sostituzione dell’angolo
orario (del sistema relativo) con l’ascensione retta (del sistema assoluto). Le
due origini differiscono per un angolo (espresso in ore: 360° = 24h) che cambia
per il verso di crescita e con lo scorrere del tempo.
L’osservazione del moto degli astri sulla volta mostra che alcuni luminari
seguono una rotazione che differisce da quella della stragrande maggioranza, a
cui viene dato il nome di stelle. Sono i pianeti (la cui etimologia dal greco
significa proprio errante). Uno dei casi più eclatanti è quello del
Sole. Se ne accorse, forse per primo, Anassimandro (610-547 a.C.) a cui
gli si deve la scoperta dell’obliquità dell’eclittica, cioè del cammino del
Sole nel cielo. Questa scoperta non è poi così ininfluente perché evidenzia
come mentre la posizione assunta oggi dalle stelle è identica a quella di
domani ad un’ora diversa, la posizione assunta oggi dal Sole non si ripresenta
domani.
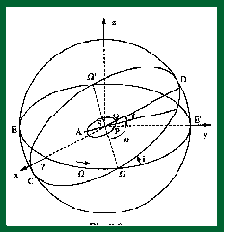
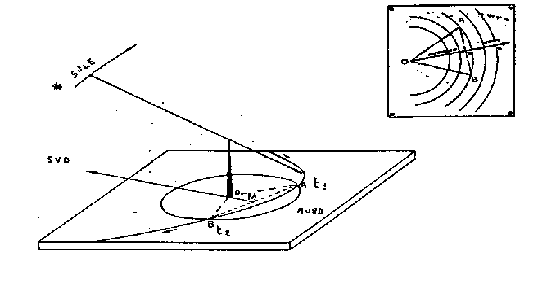
Per una serie di misure che hanno per riferimento il Sole risulta utile
costruire un sistema di riferimento relazionato ad esso (figura 8). I piani
sono l’eclittica (cammino apparente del Sole, dove hanno luogo le eclissi) ed
il piano normale al primo passante per i punti gamma e libra (le intersezioni
dell’eclittica con l’equatore celeste). Le coordinate si chiamano latitudine e
longitudine eclittiche. Il piano eclittico appare inclinato di i =
23°26’24” rispetto all’equatore celeste, il polo punta nella costellazione del
Drago a a = 18h; d = 66°33’36” (cioè 90°- i).
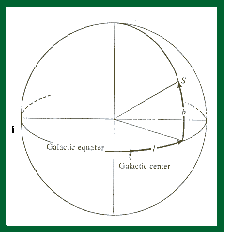
In alcuni contesti può risultare utile un ulteriormente diverso sistema di
riferimento, detto sistema di riferimento galattico (figura 9). Si tratta di un
sistema assoluto, analogo a quello equatoriale o eclittico, le cui coordinate
prendono origine da due piani tra loro perpendicolari. Il piano di riferimento
principale è quello della Galassia e l’intersezione nel presunto centro
galattico, a coordinate equatoriali assolute a =
17h39m18s; d = -28°54’ (epoca 1900.0). Le coordinate riferite a questi
piani sono la latitudine e la longitudine galattiche. Il numeretto che segue
l’epoca è l’anno in cui quelle coordinate sono rigorosamente corrette (nella
fattispecie, il 1900). Infatti, come accenneremo più avanti, il sistema
equatoriale assoluto ha come riferimento il Sole, tiene cioè fisse le proprie
coordinate rispetto al moto del Sole. In realtà le stelle hanno un piccolo moto
proprio rispetto a queste coordinate (si tratta in realtà di un moto della
Terra che prende il nome di precessione dell’eclittica e che fu scoperto da
Ipparco nel II sec. a.C.), pertanto il centro galattico vede cambiare le
coordinate al passare delle epoche.
Possiamo riepilogare dicendo che: tutti i sistemi di riferimento trattano
la volta celeste come una cupola e si disinteressano dell’eventuale differenza
di distanza degli astri; tutti i sistemi di riferimento hanno per origine, nel
calcolo delle coordinate, due piani perpendicolari tra loro che intersecano la
volta celeste in due cerchi massimi; il sistema di riferimento altoazimutale ed
il sistema di riferimento equatoriale relativo hanno le coordinate che
dipendono in tutto o in parte dal luogo dell’osservatore; i sistemi equatoriale
assoluto, eclittico, galattico sono assoluti e le coordinate dipendono solo
dalla posizione in cielo dell’astro, riferita a diversi piani di riferimento, a
seconda di quale sistema si stia adottando. La scelta dei sistemi di riferimento ha privilegiato l’aspetto spaziale, il
passo successivo consiste nel congiungerlo con quello temporale che, abbiamo
detto, è più semplice da trattare in quanto monodimensionale, ma non per questo
banale. I moti degli astri si sono rivelati gli orologi più precisi per un
lunghissimo intervallo di tempo. Quali fenomeni astronomici sono stati scelti?
L’alternarsi del giorno con la notte, l’alternarsi delle stagioni, le fasi
lunari, la rotazione delle stelle sulla sfera celeste. I moti degli astri in
genere sono stati i migliori orologi di cui l’uomo ha disposto anche per tutte
le applicazioni pratiche fino all’800. Solo nel XX secolo si sono avuti dei
segnatempo più affidabili. Non a caso fino al ‘900 le definizioni operative
della fisica si basavano sui moti celesti. In una civiltà rurale come era
essenzialmente quella romana, l’intervallo di tempo era l’ora, la dodicesima
parte (retaggio babilonese) dell’arco diurno del Sole per il giorno ed i
quattro turni di guardia (le vigilie) durante la notte. Quindi è divenuto
campione di riferimento la 3 600-esima parte (un altro retaggio babilonese)
dell’ora, il secondo. Dapprima definito come 86 400-esima parte del Giorno
Solare Medio (GSM). Poi quando ci si è accorti che il giorno si allungava
progressivamente si è passati ad altra definizione. Quelle attuali si basano
sulle leggi della fisica atomica (1 s = 9 192 631 770 transizioni del cesio-133).
Il numero prende origine dalla scelta di rendere i due tempi coincidenti in un
giorno preso come riferimento per il passaggio da uno all’altro sistema. Abbiamo detto Giorno Solare Medio. Ma cosa è? E’ esperienza banale
osservare che il Sole compie un arco in cielo diverso a seconda delle stagioni.
D’estate le giornate sono più lunghe, cambiando istante e posizione del sorgere
(e del tramontare). La massima altezza (culminazione) viceversa avviene sempre
nella stessa direzione (a sud per tutti i luoghi della Terra sopra il tropico
del Cancro, a nord per tutti i luoghi a sud del Tropico del Capricorno).
Scegliere il transito come l’istante d’inizio porta numerosi vantaggi. Su
questa considerazione si basa il Giorno Solare Vero (GSV) definito come l’intervallo
di tempo che intercorre tra due passaggi in culminazione del Sole (scelgo la
culminazione inferiore per non avere il cambio di data nel bel mezzo delle
attività diurne). Niente comunque mi impedirebbe di scegliere la culminazione
superiore e di aggiungere 12 a posteriori. Dato che la culminazione avviene al transito in meridiano questo intervallo
di tempo coinciderà per tutti i luoghi che condividono lo stesso meridiano ma
sarà diverso per luoghi anche vicini ma su meridiani diversi. Il GSV ha quindi
un significato locale. Il GSV, oltre ad essere locale, presenta ulteriori
inconvenienti. Utilizzando dei mezzi meccanici di misura ci si accorge che la
durata di questo intervallo varia nei diversi periodi dell’anno (si noti di
passaggio che aver detto “varia” rivela che non è stato scelto il GSV come
riferimento fisico del tempo). Per ovviare a questo inconveniente è stato
definito un Sole Medio che parte dal punto gamma e arriva negli stessi istanti
del Sole Vero ma che si muove sull’equatore a velocità costante. Si sono così
eliminate le variabilità dovute all’inclinazione dell’eclittica e la velocità
orbitale variabile della Terra. Si ha così un Tempo Solare Medio (TSM) che è
basato sul Giorno Solare Medio (GSM), ovvero l’intervallo di tempo che intercorre
tra due passaggi in culminazione del Sole Medio (è il tempo scandito dagli
orologi, ma non l’ora dell’orologio). Solo tra due passaggi in culminazione del
Sole Medio passano sempre 24 ore. Abbiamo così risposto alla domanda che ci eravamo posti in precedenza.
Tuttavia, anche solo di passaggio, possiamo evidenziare come il GSM risolva
alcuni problemi, creandone altri. Prima della definizione atomica del tempo,
l’orologio più affidabile era lo strumento che si rifaceva direttamente al moto
degli astri. Uno di essi, sicuramente quello più usato e diffuso, era la
meridiana (fugura 10). Ma una meridiana funziona col Sole Vero e segna il Tempo
Solare Vero (TSV), non quello medio, a meno di opportune correzioni, dal
momento che l’ombra è naturalmente prodotta
dal Sole Vero che coincide con
quello Medio solo all’equinozio di primavera. La differenza varia in funzione
del giorno e si chiama Equazione del tempo ed è pari a E = TSV-TSM.
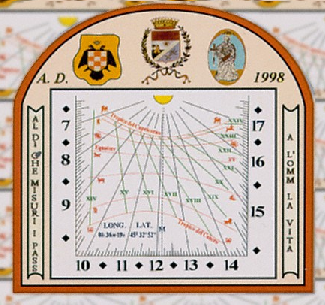
Lo scostamento tra il mezzo del giorno ed il mezzogiorno viene talvolta
riprodotto graficamente su alcune meridiane. Si tratta di una linea chiusa a forma di “8” che prende il nome di analemma
(figura 11). Scandito sul Sole Medio con inizio alla mezzanotte (requisito di
fatto oggi adottato da tutti i paesi anche se non necessario) e riferito ad una
località significativa dal punto di vista civile, anche se totalmente estranea
dal contesto geografico-astronomico è il Tempo Civile (TC), reso necessario per
le comunicazioni fra località, anche significativamente distanti, che non
potevano essere regolate, è proprio il caso di dire, sullo stesso campanile. Quasi tutte le attività umane sono scandite dal Sole Vero, ma il numero
crescente di interconnessioni fra i vari centri urbani (vie commerciali prima,
treni e telegrafi poi) ha reso necessario standardizzare i tempi. Nel corso
della storia si adottarono ore di uguale durata (scostamenti di frazione d’ora
per le attività pratiche non sono significativi) con inizio alla mezzanotte di
Tempo Civile. In Toscana un editto dei Lorena impose il passaggio alle ore
“alla francese” nel 1749, come già in vigore in molti altri paesi europei. E’
curioso notare come gli uffici pubblici, dal 1 gennaio 1749 fossero obbligati
ad adottare il nuovo sistema nel computo del tempo, sotto la minaccia di multe
salate a chi avesse trasgredito. Tuttavia il mondo contadino continuava a
togliersi il cappello all’Ave Maria della sera, che segnava il passaggio da un
giorno al successivo, e pure le meridiane continuavano a riportare ancora le
ore all’italiana, se non in maniera esclusiva per lo meno in aggiunta (si veda
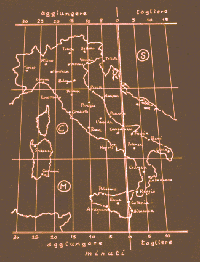
nella precedente figura 10 le due serie di linee orarie). L’Italia unita adottò un tempo medio per tutta l’Italia col Regio Decreto
3224 il 22 settembre 1866. Il decreto escludeva le isole che invece avrebbero
seguito il tempo civile rispettivamente di Palermo e di Cagliari.
L’unificazione su un solo tempo civile avvenne nel 1893 (figura 12) con
l’ingresso nello Standard Time, il tempo del meridiano di 15° di
longitudine est. Ma per territori più ampi di una regione? E per diversi stati? Negli Stati
Uniti nel 1870 si avevano 50 diversi orari (e ogni compagnia ferroviaria
seguiva la propria ora). Si rendeva necessario uniformare tutto il Paese, ma
d’altra parte una sola ora fra Atlantico e Pacifico rendeva troppo stridente il
contrasto col Sole Vero. Nel 1859 il bolognese Quirico Filopanti aveva proposto
di suddividere la Terra per mezzo di meridiani. Poiché 360°/24h = 15°/h
possiamo dividere la Terra in 24 spicchi detti fusi di 15°. Le ore dei
meridiani 15°, 30°, 45°, … stabiliscono l’ora di tutto il fuso, differente di
un’ora da quella del contiguo. “Quando un orologio… batterà un’ora
qualunque, tutti gli orologi del Mondo … suoneranno in quel medesimo istante, e
indicheranno o quella stessa ora od una qualunque altra ora intera.” (Q.
Filopanti).
In una conferenza del 1879, spinta dalle pressanti esigenze soprattutto di
compagnie come la statunitense American Railway Association, si stabilì
l’adozione dello Standard Time = tempo di Greenwich, più o
meno un numero intero di ore, di fatto l’attuazione dell’idea di Filopanti,
anche se un po’ sgarbatamente il suo nome non fu ricordato, tanto da essere
noto oggi solo agli studiosi dell’argomento (d’altra parte gli USA hanno impiegato
ben oltre un secolo per riconoscere i meriti di Meucci nell’invenzione del
telefono...). Oltre agli Stati Uniti, principali fautori, quasi tutti i paesi del Mondo
aderirono nel giro di pochi anni. L’Italia aderì nel 1893. Nel 1897
praticamente tutta Europa aveva aderito (anche la Francia adottò il tempo di
Greenwich, ma la ruggine della vittoria di Wellington sulle truppe napoleoniche
e lo sciovinismo innato transalpino spinsero a dichiarare ufficialmente che si
trattava del tempo di Parigi ritardato di 9m21s!). Oggi tutti paesi del Mondo
hanno adottato, almeno per le transazioni internazionali, il principio dei fusi
orari, anche se esigenze civili fanno sì che talvolta l’ora di alcuni distretti
è quella del fuso adiacente (figura 13). In astronomia per uniformarci si elegge il TC di un particolare fuso come
quello universalmente rappresentativo (Tempo Universale, TU). E’ stata una
scelta pressoché obbligata quella di prendere il meridiano passante per
Greenwich, discriminante fra zona est ed ovest del Mondo. A molti dei problemi riguardanti il moto “irregolare” del Sole si può
ovviare con un’altra scelta del fenomeno ripetitivo segnatempo: prendendo per
esempio il moto di una stella scandito dal transito in meridiano. Si tolgono di
mezzo i problemi inerenti alla variabilità della velocità orbitale terrestre ed
all’inclinazione dell’eclittica. Questo è il cosiddetto Tempo Siderale. Poiché
ogni località ha un meridiano proprio anche il Tempo Siderale ha un significato
locale (da cui l’abbreviazione TSL) e si calcola come: TSL = H+a, dove H è
l’angolo orario e a l’ascensione retta (presente sui cataloghi e le
carte del cielo) della stella. Analogamente al TU si definisce un tempo
siderale assoluto (TSG) rappresentativo della Terra il TSL del meridiano di riferimento
prescelto (ancora una volta quello di Greenwich). Nel tempo che la Terra compie una rotazione attorno al proprio asse ha
avanzato pure lungo l’orbita. Perché il Sole ritorni in meridiano (Giorno
Solare Medio) occorrerà un tempo maggiore di quella che occorre ad una stella
(Giorno Siderale) che, essendo “a infinito” non risente dei moti orbitali
terrestri Poiché il Sole impiega un anno tropico (che dura 365.2422 GSM) a
ritornare nel punto gamma ogni giorno c’è un ritardo del Sole rispetto alle stelle
di 360°/365.2422 = 24h/365.2422 = 3m56s. Poiché le nostre 24 ore sono scandire
sul giorno del Sole, il Giorno Siderale dura 24h-3m56s = 23h56m4s. Per praticità, in ambito astronomico, è stata adottata pure un’altra
grandezza, il Giorno Giuliano, definito come numero progressivo di giorni
intercorsi dal 1 gennaio del 4713 a.C., alle ore 12 di TU. Si tratta di un
giorno di durata coincidente con quello medio ma che si differenzia per essere
indipendente dalla scansione calendariale degli anni, dei mesi, delle
settimane. Joseph de l’Escale de Bordons (1540-1609) ideò il Giorno Giuliano in
cui ogni giorno ha un’unità più del precedente. L’inizio fu stabilito quando
coincisero gli inizi dell’indizione romana (15 anni), che oggi ha solo valenza
liturgica, ciclo solare (di 28 anni), numero d’oro (di 19 anni) legato al ciclo
lunare. La prima tornata della data giuliana, “l’anno giuliano”, per così dire
(senza fare confusione col vero anno giuliano che sancì l’attuazione della
riforma del calendario e che introdusse l’anno bisestile), si concluderà il 22
gennaio 3267. Come posso sapere la posizione del Sole sapendo l’ora (e ovviamente la
data)? L’ora e la data danno le coordinate (angolo orario ed ascensione retta) TSL=Hv+av=Hm+am ; Hv– Hm =av– am =
E; av = E+am Gli antichi potevano fare una misura diretta del Sole? No, si affidavano
alla distanza rispetto alle stelle. Così non si accorsero che molto tempo
dopo am in realtà variava: si trattava del fenomeno di precessione
degli equinozi, che scoprirono difatti in un’altra maniera, ed in un certo modo
aumenta ancora più la nostra ammirazione per Ipparco che se ne accorse nel II
sec. a C.
Svariati furono gli strumenti usati per la misura del tempo. Sicuramente
quelli più rinomati ed anche più appariscenti furono le meridiane che
assolvevano al duplice scopo di segnare sia lo scorrere del tempo nella
giornata, sia la stagione dell’anno. Le meridiane che nascono in Grecia avranno
largo impiego e diffusione ovunque, restando gli orologi più precisi per tutto
il XIX secolo. Nel ‘500 avevano avuto una certa diffusione gli orologi
meccanici (uno dei primi è quello di Palazzo Vecchio a Firenze, datato 1353),
evoluzione degli svegliarini monastici utilizzati nel Medioevo dai monaci per
le preghiere notturne, ma la loro affidabilità era scarsa. Le meridiane più
semplici sono quelle piatte orizzontali o verticali, ma ci sono anche altri
modelli equatoriali, concave, convesse e perfino a rifrazione, senza
considerare il largo impiego delle navate delle chiese come camere oscure, una
variante al principio base della meridiana, che si fondano sul principio di
proiettare l’ombra (o un pennello di luce nel caso delle camere oscure) su una
superficie di riferimento. Si tratta dunque di strumenti basati sulla geometria
proiettiva, non poi troppo complicate da realizzare, tanto che alcuni artigiani
si dilettavano a costruirne di sempre più complesse, sulle superfici più
disparate per dimostrare la loro competenza in fatto di geometria, più che per
una reale utilità. Anche altri strumenti come l’astrolabio (figura 14), che può
essere usato anche come orologio e calendario, si basa su una geometria
proiettiva (il che induce delle deformazioni nell’aspetto del cielo come ad
esempio l’orizzonte che in certi modelli ha due cuspidi). Il notturlabio, o
notturnale (figura 15), invece non si basa sulla proiezione. Esso è capace
difatti di indicare l’ora a partire dall’osservazione diretta della posizione
di alcune stelle dell’Orsa Maggiore (sempre visibili essendo circumpolare) in
riferimento alla Polare, assai prossima all’asse polare già da alcuni secoli.
Come si può facilmente intuire, il cielo, osservato attraverso l’occhio
nudo, è stato capace di dare all’uomo anche l’orientamento. Un semplice bastone
piantato nel terreno (che per inciso può essere lo gnomone di una meridiana
orizzontale) è capace di dare l’asse nord-sud e di conseguenza il piano
meridiano. Basta tracciare un cerchio di opportune dimensioni concentrico alla
base del bastone ed attendere che l’ombra al mattino ed al pomeriggio intersechi
la circonferenza. Si tratta del cosiddetto cerchio indiano (figura 16).
Entrambe le bisettrici tra i due punti di intersezione sono sull’asse meridiano
(una a nord, l’altra a sud). La precisione della determinazione dipende dalle
dimensioni dello gnomone e dal contrasto della sua ombra sul piano, comunque
ben difficilmente si ottiene una precisione inferiore a quella di una bussola
che, per l’Italia, declina ad ovest di un paio di gradi (il valore varia da
zona a zona ed anche in funzione del tempo) poiché punta verso il polo nord
magnetico, discosto dal polo geografico di una decina di gradi. Comunque sia la
bussola ha avuto la sua grande utilità, specie in marina, anche in virtù di non
essere soggetta ai capricci del tempo.
Una volta ottenuto l’asse meridiano (la cui utilità si riflette anche sulla
misura del giorno solare) l’uomo ha cominciato ad interrogarsi sulle dimensioni
e la forma dell’oggetto su cui viveva. Secondo gli Egizi, i Babilonesi ed il
filosofo greco Talete (634-548 a.C.) la Terra è il “pavimento” di una scatola
ed è quindi piatta. Nel circolo degli iniziati della scuola pitagorica tuttavia
comincia a prendere corpo la concezione cosmologica secondo la quale la Terra è
sferica e ruota, come il Sole e gli altri pianeti, attorno ad un fuoco
centrale. L’idea è dello stesso maestro, Pitagora (571-496 a.C.), o
dell’allievo Parmenide (520-440 a.C.). Da allora in poi (salvo la pausa
medievale) gli eruditi sono convinti della sfericità del nostro pianeta. Anche
Aristotele ne è convinto e porta a testimonianza l’altezza delle stelle alle
diverse latitudini, la vista delle navi all’orizzonte, la forma dell’ombra
delle eclissi lunari. Le obiezioni a Cristoforo Colombo nel XV secolo
(rivelatesi poi fondate) riguardavano le distanze non la sfericità.
Se dunque la Terra è una sfera la sua cartografazione può essere fatta
sulla falsa riga della cartografazione celeste (figura 17). Tralasciamo il
discorso della distanza dal centro e con due soli parametri siamo in grado di
stabilire in maniera univoca un punto sulla superficie. Le due coordinate che
prendono origine dal cerchio massimo detto equatore e da un meridiano d’origine
si chiamano latitudine e longitudine. Numerosi sono i metodi astronomici
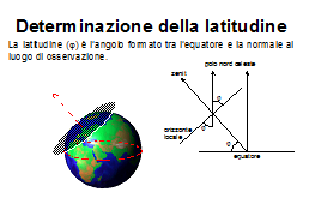
impiegabili per determinare le due grandezze. La latitudine si misura con
numerosi strumenti che generalmente calcolano un angolo. L’altezza della Polare
(figura 18), il Sole a mezzogiorno, ma anche l’altezza di una qualunque stella
sono in grado di fornire la latitudine del luogo di osservazione, a patto di conoscere
la declinazione dell’astro. La formula generale è j = h(N)+d-p/2,
dove j indica la latitudine, h l’altezza (contata a
partire dall’orizzonte nord), d è la declinazione
dell’astro, p/2 è una costante, pari ad un angolo retto, espresso in
radianti (a patto di esprimere anche le altre grandezze in radianti). La
longitudine è sicuramente più complessa da determinare, anche se la formula
rimane piuttosto semplice, non essendoci un riferimento astronomico univoco
(difatti la scelta dello zero su Greenwich è puramente convenzionale, non a
caso nel corso dei secoli lo zero è passato per Alessandria, per le isole
Fortunate – Canarie –, per le
Azzorre e così via). L’espressione è l
= TSG-TSL, dove l indica la longitudine
mentre TSG e TSL i tempi siderali di Greenwich e locale. La difficoltà risiede
nel fatto che mentre sono qui ad osservare non posso essere anche a Greenwich e
se fossi ad osservare a Greenwich non sarei qui. L’occhio nudo mi consentirebbe
di determinare la longitudine se contemporaneamente un altro dispositivo mi
fornisce il tempo siderale di Greenwich. Fino a metà del XVIII secolo anche col
bel tempo la longitudine era un problema in apparenza senza speranza in quanto
non esisteva orologio capace di mantenere in mare l’ora precisa del porto di partenza.
Un secondo sgarrato comporta 15” d’arco, una deriva di mezzo chilometro ad
oriente, se anticipa, a occidente se ritarda. Per raggiungere un porto mi
potrei accontentare di un errore contenuto nella decina di secondi, ma per
evitare scogliere o bassi fondali un paio di secondi sono fondamentali. Citiamo
qualche episodio e l’epilogo per dovere di completezza anche se esula dal
periodo dell’osservazione del cielo ad occhio nudo (lo stesso Galileo,
inventato il telescopio, aveva proposto il celatone, un sistema che faceva uso
di un cannocchiale).
Si racconta che sir Clowdisley Shovell, al comando della propria flotta,
stava tornando vittorioso verso Londra dopo alcune schermaglie con le navi
francesi dalle parti di Gibilterra. Era il mese di ottobre del 1707. In base
alle valutazioni del punto stimato, tutti gli ufficiali di rotta erano
d'accordo con l'ammiraglio che la flotta si trovasse ad ovest dell'isola di
Ouessant, una delle isole al largo della Bretagna, ed era convinzione generale
che le navi fossero in acque profonde e quindi al sicuro. Purtroppo cadde la
nebbia e le navi furono costrette a muoversi senza che le vedette potessero
scorgere eventuali pericoli. I calcoli erano sbagliati, le navi erano
pericolosamente vicine alle isole Scilly, contro le quali andarono ad urtare
nella notte del 22 Ottobre (figura 19). Di una flotta di cinque navi da guerra
ne affondarono quattro, portando negli abissi migliaia di uomini. Due persone
si salvarono, una di queste fu proprio l'ammiraglio che, mentre guadagnava con
fatica la riva, senz'altro avrà pensato a quel marinaio che aveva fatto
impiccare il giorno prima. Quel marinaio aveva osato, per proprio conto,
calcolare la posizione delle navi ed essendosi convinto che esse fossero
pericolosamente vicine alla costa, aveva avvertito l'ammiraglio. L'ammiraglio,
applicando le regole della marineria militare inglese, lo aveva fatto
immediatamente impiccare, infatti nelle regole di ingaggio era esplicitamente
proibito ai marinai di rilevare la posizione delle navi. Una volta giunto a
riva, l'ammiraglio venne ucciso da una contadina del luogo, innamorata
perdutamente dell'anello di smeraldo che Shovell portava al dito. Ma questo si
seppe solo quando la stessa contadina, presa dal rimorso confessò, in punto di
morte, il delitto al suo Pastore, portando in prova l'anello rubato
all'ammiraglio.
La determinazione della longitudine era una questione di rilevanza
strategica, economica e militare, tanto che il Parlamento inglese, per evitare
altre sciagure come quella delle isole Scilly, emise un bando nel 1714, con un
premio di 20 000 sterline a chi fosse riuscito nell’impresa di scovare un
metodo per determinare la longitudine in mare. La perizia e l'ingegno di un
orologiaio di nome John Harrison portarono a compimento un segnatempo il quale
raggiunse il 19 gennaio 1762 le coste della Giamaica, perdendo 5 secondi dopo
81 giorni di navigazione. La sfida era stata vinta. Fanno parte dell’aneddotica
i risvolti poco nobili degli astronomi che si arrampicarono sugli specchi pur di
non decretare la vittoria di un orologiaio. Le date mostrano comunque in
maniera inequivocabile che la questione della longitudine, soprattutto in mare,
fu un problema che si risolse senza telescopio ma in piena era telescopica. Se da un lato la longitudine in mare aperto era una spina nel fianco della
scienza, visto che il rollio ed il beccheggio di una nave (oltre ai problemi di
variazione di temperatura, pressione, umidità) non consentivano ad un orologio
di mantenere l’ora, essa poteva essere rilevata con una certa precisione su un
luogo fisso come un’isola, avendo a disposizione tutto il tempo necessario,
aspettando che si verificasse un evento, visibile contemporaneamente anche da
Greenwich. Occasioni del genere non mancavano. Si trattava delle eclissi. Anche
Cristoforo Colombo avrebbe potuto scoprire l’America se fosse stato capace di
eseguire correttamente la rilevazione di una eclisse lunare avvenuta nel 1509 e
di interpretare correttamente le tavole del Regiomontano di cui disponeva (le
malelingue sostengono che in realtà Colombo le aveva interpretate bene ma
finse, con un camuffamento dei dati, per riportare in Spagna l’idea di essere
arrivato davvero nei pressi del Cipango, invece di non essere neanche a metà
strada). In ogni caso degli astri l’uomo si è servito per determinare anche le
dimensioni dell’ambiente in cui vive, cominciando dalla Terra. Longitudine e
latitudine a parte si tratta di determinare il terzo parametro, la famosa
distanza dal centro.
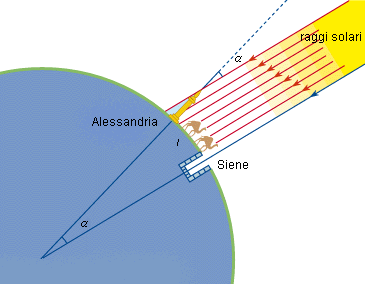
Eratostene di Cirene (276-196 a.C.) fu probabilmente il primo a concepire
l’idea di misurare la Terra, in un’ottica di sfericità acquisita. Non ci è
giunta l’opera originale di Eratostene e non sappiamo nemmeno, se non per linee
generali, quale procedura adottò. Sicuramente comunque la sua fu una misurazione
di differenza di altezza del Sole al solstizio, da due diverse località. Egli
sapeva che durante il solstizio d’estate la luce del Sole penetrava nei pozzi
profondi di Syene, mentre ad Alessandria un lungo obelisco proiettava una certa
ombra (figura 20).
Il risultato ottenuto fu di 250.000 miglia per il meridiano terrestre,
probabilmente qualcosa dell’ordine dei 39 400 km, un risultato
sorprendentemente vicino al vero (L = 40 009 km). Nell’ipotesi di Terra sferica
il raggio risultava di 6 270 km (contro i 6 370 km circa). Nel I secolo a.C. Posidonio di Canapea propose una nuova misura del
meridiano terrestre, sulla falsariga di Eratostene. Egli propose di osservare
l’altezza di una stella (nella fattispecie Canopo) da due località, Rodi ed Alessandria,
e di determinare la loro distanza mediante i resoconti dei marinai che
percorrevano quella rotta. Anche se in linea di principio il metodo era
altrettanto valido di quello di Eratostene ottenne un valore meno preciso (L =
37 800 km) perché non era a conoscenza dell’effetto della rifrazione che alza
la posizione degli astri riducendo la differenza angolare delle misure. Per il mondo occidentale la storia si interrompe, una nuova determinazione
arriverà dopo l’oblio medievale solo nel XVII secolo. Durante questo lungo
periodo sono gli Arabi l’avanguardia del progresso scientifico. Nel 827
l’astronomo arabo Al Mamum propose una nuova determinazione del meridiano
terrestre. Allo scopo vennero effettuati sopralluoghi nella piana di Sindjar,
valutando l’altezza del Sole ai due estremi e poi calcolando la distanza delle
postazioni. A differenza di Eratostene e Posidonio, che avevano sfruttato i
resoconti di altri per la determinazione della distanza, in questo caso il
calcolo ebbe come finalità prioritaria la determinazione scientifica. Il
risultato fu di circa 38 600 km, un valore un po’ sottostimato. Nel 1614 Snell (1580-1626) effettuò una triangolazione dei territori
olandesi dalla quale ottenne L = 38 600 km. Nel 1633 Riccardo Norwood eseguì un
lavoro geodetico fra Londra e York ottenendo L = 40 200 km. Nel 1669 Jean
Picard eseguì una triangolazione francese ed ottenne L = 40 033 km. Nello
stesso anno intanto Huygens sospettò la non sfericità della Terra,
ipotizzandone uno schiacciamento ai poli. Per comprovare, o smentire, l’ipotesi
di Huygens molti scienziati ed astronomi vennero inviati ad eseguire campagne
di rilevazione. Se la Terra è schiacciata l’arco di meridiano in prossimità
dell’equatore è più lungo che al polo. Così l’Accademie de Sciènces inviò
Bourguere e La Condamine in Perù (1735) e Maupertuis in Lapponia (1736); in
Italia troviamo impiegati, Zannoni, Inghirami, Boscovich e Maire (1750). Di
nuovo finiamo fuori “tempo massimo”. L’era del cielo ad occhio nudo era finita
da oltre un secolo. Difatti per le loro campagne di rilevazione gli scienziati
si avvalevano di strumenti quali l’odometro, la tavoletta pretoriana e piccoli
telescopi. Di tanto in tanto allestivano anche piccoli osservatori da campo.
Non pago di determinare la misura della Terra l’uomo ha cercato di misurare
anche il cosmo. Il primo metodo ha sfruttato la parallasse, cioè la diversa
angolazione con cui si guarda un oggetto, rispetto ad uno sfondo lontano, in
virtù della distanza tra i due punti di vista.
Certamente il primo astro a finire sotto il vaglio degli scienziati è stato
il corpo che ha dato la sensazione di essere il più vicino: la Luna. Alla
distanza a cui si trova la parallasse sfiora 1°. Si tratta di un valore
piccolo. Per la precisione con cui i Greci potevano stimarla avrebbero ottenuto
errori troppo grandi, per cui utilizzarono poco questo metodo, anche se vedremo
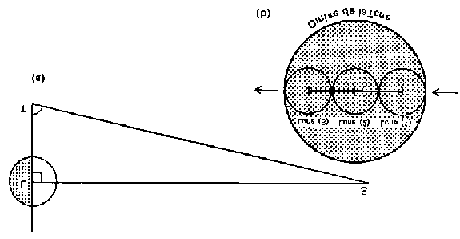
che Ipparco lo tentò con successo (figura 21). Aristarco ipotizzò di sfruttare
le eclissi in un processo a due fasi: nell’ipotesi di Sole “a infinito”, se si
comparano le dimensioni dell’ombra terrestre e della Luna, si ottiene un raggio
lunare pari a circa ¼ di quello terrestre (figura 22). Col raggio che poi
Eratostene avrebbe calcolato si ottenevano 1 570 km (contro i 1 738 delle stime
attuali). Comparando quindi le dimensioni angolari della Luna con le dimensioni
effettive appena calcolate otteneva pure la distanza. Il valore ricavato da
Aristarco fu di circa 60 raggi terrestri, un valore assai prossimo al vero.
Già i Greci, oltre che della Luna, si erano presi cura di calcolare anche
la distanza del Sole, riuscendo però assai peggio nell’impresa. Sempre
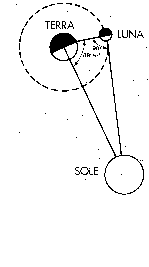
Aristarco aveva proposto il metodo della dicotomia solare. La Luna al quarto
non occupa la stessa posizione che occupa a metà strada fra il primo e l’ultimo
quarto a causa della distanza finita del Sole, differisce di circa 8’ = 0.15°
(figura 23). Aristarco rilevò invece uno scarto di 3° ottenendo una distanza,
rispetto all’orbita della Luna, 19 volte maggiore (il valore corretto oggi è
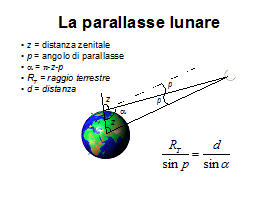
390 volte maggiore). Ipparco di Nicea (188-125 a.C.) sfruttò il metodo della
parallasse lunare, per la quale ottenne 53’, e la combinò con l’eclissi per
determinare le dimensioni effettive della Luna. Mediante la dicotomia, come
aveva fatto Aristarco, giunse ad una stima di distanza del Sole di 1 100 raggi
terrestri (oggi sappiamo essere 23 500). Siamo ancora lontani ma ci si muove
nella giusta direzione. A posteriori, con la misura di Eratostene,
sarebbe giunto ad una distanza di 7 milioni di km. La stima di Ipparco per quanto
fuori misura era comunque sufficiente a stimare le dimensioni del Sole pari ad
almeno cinque volte il globo terrestre (vuol dire che era sicuramente più
grande del Peloponneso come aveva suggerito Anassagora, sia pure su
considerazioni erronee come la piattezza della Terra, tre secoli prima!).
Copernico, ben sedici secoli più tardi, a testimonianza della pochezza di
risultati nell’intermezzo medievale, si attesta sugli stessi valori. Keplero si
avvicina di più facendo affidamento sulle osservazioni di Tycho Brahe. Affermò
che il Sole ha una parallasse minore di quella di Marte che è 1’. Quindi il
Sole dista più di 20 milioni di km, ma ciò che più conta dell’opera di Keplero
è che mediante la sua terza legge sul moto dei pianeti è possibile determinare
la corretta scala delle distanze nel sistema planetario. I metodi telescopici
dei secoli successivi portarono ad una stima sempre più prossima ai canonici
149.6 milioni di km, ma l’osservazione ad occhio nudo della posizione dei
pianeti, in tempi diversi, congiunta con le leggi di Keplero consentiva già di
stabilire le dimensioni di tutte le orbite in rapporto all’orbita terrestre.
Un laboratorio dell’astronomia non può tacere uno degli aspetti salienti,
vale a dire la stima della luminosità degli astri, stima che per secoli l’uomo
ha dovuto eseguire col solo occhio nudo. La magnitudine apparente è un
parametro che stabilisce la luminosità percepita di una stella. Il termine
magnitudine richiama la grandezza. Infatti, ipotizzando che le stelle fossero
tutte alla stessa distanza, la luminosità e la grandezza erano in relazione
diretta. Forse il primo che ebbe l’idea di catalogare le stelle secondo la loro
luminosità fu Ipparco. Nonostante i progressi tecnici, moltiplicatisi
esponenzialmente nell’era moderna, solo dalla seconda metà dell’800 fotometri
sempre più precisi hanno soppiantato l’occhio umano nella determinazione della
magnitudine stellare. Prima si procedeva ad occhio nudo con la tecnica di
Argelander. Nel II sec a.C. Ipparco suddivise le stelle in 6 classi di
luminosità (magnitudini) (la figura 24 riporta un estratto medievale dove al
nome arabo ed alla posizione della stella, segue la magnitudine e pure
l’affinità cromatica col pianeta corrispondente). Il metodo di Argelander per
costruire un catalogo stellare che avesse sempre 6 classi di luminosità
consisteva nel confrontare le stelle a coppie. La differenza è una magnitudine
quando le due stelle, al primo colpo d’occhio, sembrano uguali e solo dopo un
certo tempo ci si accorge che una è più luminosa dell’altra; 2 magnitudini
quando le due stelle sembrano uguali al primo colpo d’occhio ma subito dopo si
nota una differenza; 3 magnitudini quando già al primo colpo d'occhio si nota
una certa differenza; 4 magnitudini quando al primo colpo d'occhio la differenza
è ben evidente; 5 magnitudini quando si ha un'evidente sproporzione di
luminosità fra le componenti della coppia in esame. Ripetendo più e più volte
la misura in notti diverse e mediando per un numero arbitrario di coppie si
ottiene un catalogo completo quanto si desidera ed accurato. Va prestata
attenzione al colore delle stelle che può falsare la stima, in quanto l’occhio
umano ha una diversa risposta alle varie frequenze. La risposta massima si ha
intorno al giallo. La fotometria moderna, oltre a consentire l’apprezzamento di
frazioni di magnitudine, ha constatato che il metodo di Argelander rispetta una
legge di potenza. In altre parole l’occhio umano ha una risposta logaritmica. Prof. Lorenzo Brandi KEPLERO IL PREVEGGENTEGalileo Galilei, con l’introduzione del suo cannocchiale, aveva rivoluzionato il modo di fare astronomia che adesso diventava assai più osservativa. Nel marzo 1610 scrive il Sidereus Nuncius e gli epistemologi lo giudicano un testo scritto in fretta e furia per timore che qualcuno gli soffiasse le scoperte che intanto andava facendo. Ed i suoi sospetti erano tutt’altro che infondati visto che il tedesco Simon Mayr ci provò a rivendicare la priorità nella scoperta dei satelliti medicei. Per questo motivo Galileo, che nel
frattempo continuava a fare scoperte, affinò la sua strategia inviando a giro
per l’Europa strani anagrammi nei quali celava una presunta scoperta, così che
potesse rivendicarne la paternità qualora qualche altro l’avesse fatta, permettendosi
così di poterla analizzare a proprio agio. Fu così che già nel luglio 1610 Galileo inviò presso Giuliano de’ Medici, ambasciatore del Granducato di Toscana a Praga, un anagramma: “smaismrmilmepoetaleumibunenugtaurias” e poi nel dicembre un altro “haec immatura a me jam frustra leguntur oy”. Anche se con l’aggiunta di “oy” il secondo è più carino in quanto cerca di dare un senso compiuto [Queste cose premature le studio ora invano oy]. Il primo svelava la presunta forma trilobata di Saturno, rivelatasi poi errata, e la seconda le fasi di Venere. Essi infatti, traslitterati, recitano: “Altissimus planetam tergeminum observavi”, cioè “Ho osservato l’altissimo [il più lontano] pianeta trilobato” e “Cynthiae figuras aemulatur mater amorum”, cioè “La madre degli amori [Venere] imita le figure [le fasi] di Cinzia [la Luna]”. Di passaggio si può notare l’estremo scrupolo di Galileo che per rendere più nascosta ancora la scoperta usa locuzioni di stampo classico o pagano, dicendo Cinzia in luogo di Luna, madre degli amori in luogo di Venere e pianeta altissimo in luogo di Saturno. Keplero, che già da tempo era presso la
corte boema ed aveva una grande stima di Galileo, provò a convincere il collega
pisano di svelargli l’arcano. “Vi supplico di non privarci più a lungo della
soluzione. Dovete vedere che avete a che fare con onesti tedeschi”. Poteva cioè
essere bravo a matematica ma il latino non poteva dunque essere la sua materia.
Ma fu inutile. Galileo teneva serrata la bocca. A Keplero non rimaneva altro
che mettersi pazientemente a sciogliere l’anagramma. Solo per fare qualche piccolo esercizio
matematico, la prima frase contiene 36 caratteri che, anagrammati in tutte le
soluzioni possibili, producono un qualcosa come 3,72 1041
combinazioni, cioè 372 mila miliardi di miliardi di miliardi di miliardi di possibilità.
Anche con i più potenti calcolatori di oggi ci vorrebbe un tempo superiore
all’età dell’Universo, impossibile da farsi a mente nel ‘600 se non si aveva
già qualche indizio. Ma Keplero si trovò ad esultare quando credette di aver
trovato la soluzione. La prima frase concepita da Galileo aveva almeno un
anagramma di senso compiuto. Precisamente: “Salve umbistineum geminatum Martia proles,
cioè “Salve, gemello bruciante, figlio di Marte”. Ora il fatto che una serie di
lettere possa produrre, in latino, più frasi di senso compiuto potrebbe essere
una semplice curiosità di nessun conto. Che anche la seconda variante abbia un’attinenza di natura astronomica già può essere più
rilevante. Ciò che risulta però straordinario è che Keplero, inconsapevolmente,
con questa soluzione aveva anticipato una scoperta astronomica che sarà
compiuta da Asaph Hall 267 anni più tardi. Si tratta della scoperta dei due satelliti
(figli) di Marte, Phobos e Deimos, similari per natura e dimensioni e quindi
gemelli. Naturalmente Keplero si cimentò anche
col secondo anagramma galileiano. Anche in questo caso si hanno 1040 combinazioni.
Ancora una volta l’astronomo non trovò la soluzione corretta ma di nuovo una frase
di senso compiuto e di ambito astronomico: “Macula rufa in Iove est gyratur
mathem etc”, cioè “Una macchia rossa su Giove gira matematicamente”. Sembra una
chiara allusione alla grande macchia rossa. Il problema è che il primo
avvistamento risale al 1665, oltre cinquanta anni dopo. Impossibile dunque che
Keplero l’abbia potuta vedere. Si deve trattare ancora una volta di una sorta
di premonizione. Keplero era un preveggente? Due casi su due effettivamente diventano abbastanza rilevanti dal punto di vista statistico. Ad ammantare di fascino, e anche un po’ di mistero, tutta la faccenda c’è un altro indizio che certo non depone a favore del nostro astronomo. La madre fu accusata di stregoneria e solo la fama del figlio le impedì di salire sul rogo, a fiammifero già praticamente acceso. Aveva forse preso dalla madre qualche trucco del mestiere? E’ tutto frutto del caso? Ovviamente una soluzione a queste domande non può trovare risposta. Dal punto di vista logico, lasciando alla libera interpretazione capacità esoteriche e trascendenti di Keplero, possiamo solo argomentare che in quanto a latino avrebbe fatto la gioia di ogni professore. Altro che “onesto tedesco”! ILLUMINAZIONE ... VENDESIQuesto articolo tratta di un tipo di manipolazione molto diffusa, utilizzata in parte in modo istintivo da alcuni, ma anche, grazie a pianificazione studiata, da individui che sentono il bisogno – per egoismo, brama di potere, lucro, volontà di prevaricazione, e tante altre ignobili pulsioni – di sottomettere il prossimo alla propria volontà. Non esiste, ovviamente, una linea
netta di demarcazione tra la naturale influenza che ognuno può avere nei
confronti del prossimo, e la manipolazione premeditata,
ma è certo che esistano situazioni limite che possono essere definite
sicuramente manipolazione. La prova del
reato sta sia negli intenti, che nel risultato. Se capisci che ogni volta
che una certa persona ti rivolge la parola – per quanto amichevole e cordiale
possa essere questa parola – poi salutandoti si porta via qualcosa di tuo nelle
sue tasche, allora ciò significa che hai a che fare con un furfante
manipolatore. Il suo caro saluto, il suo
sorriso, le sue chiacchiere, non sono altro che un mero strumento per carpire
qualcosa da te. Io
non sono uno psicologo, non porto statistiche né dati cosiddetti “scientifici”,
ma scrivo qualcosa che deriva, prima di tutto, da mie esperienze dirette: per
questo ci tengo a pubblicare queste considerazioni. Sono un tipo abituato ad
analizzare nel minimo dettaglio ciò che mi accade e mi circonda, e per questo
utilizzo una facoltà dell’uomo che in molti chiamano: Mente. Sono fiero di
questa mia facoltà, così come sono fiero di possedere un altro aspetto,
anch’esso direi molto comune nell’uomo: il Cuore! Mente, Cuore… sono solo
parole, che descrivono però concetti importantissimi. Il Cuore è importante. La
Mente è importante… siamo fatti così! In questi ultimi tempi, è forte la
“spinta verso l’Alto” da parte di molti. Sembra che i tempi
stiano cambiando… e che Dio ci aiuti in questo lavoro, perché sia sempre più
grande il coraggio di sconfiggere la paura, di guardare oltre la nebbia del
potere, della manipolazione di massa, alla ricerca del Sole che un giorno ci
darà la Libertà. Stiamo finalmente ascoltando il nostro intuito, e il sottile
messaggio della profondità che è in noi, al cui confronto la vita materiale che
siamo costretti a condurre, appare misera e piatta. Dobbiamo sempre fare
qualcosa e abbiamo obblighi il cui vero perché, se vogliamo analizzare a fondo
la questione, sembra risiedere proprio nel dominio che altri si ostinano ad
imporre su di noi. Siamo dominati dal “Grande Potere”,
rappresentato da istituzioni ingiuste, da un Governo impazzito, da uno Stato in
sgretolamento. Ma siamo anche dominati
da noi stessi, perché ci continuiamo a fregare a vicenda, ad ingannare,
manipolare, derubare. Purtroppo l’egoismo prende quasi sempre il
sopravvento, ed ecco che nei rapporti umani si ripetono all’infinito i mali di
sempre. Nello
specifico, la manipolazione di cui
vorrei parlare in questo articolo, è quella utilizzata come arma da un certo
“particolare” tipo di venditori. Non sono i venditori classici, che
lavorano come commessi in un negozio, o che suonano alla tua porta con il
“Folletto” (aspirapolvere) in mano. Questi venditori hanno un potere di
manipolazione, tutto sommato, abbastanza limitato ed evidente, perché il loro
intento è dichiarato a priori. I venditori del tipo più pericoloso sono
piuttosto quelli che compaiono
all’improvviso nella tua vita, magari via Facebook, preceduti da un’aura di
novità e apparente simpatia “virtuale” che difficilmente non farà breccia nelle
tue difese. Qualche
messaggio, una domanda, quattro risposte, un paio di “Mi piace”, ed ecco fatto
miei cari Amici, la fascinazione programmata ha già prodotto il suo effetto. Tra un “Ciao Caro”, e un “Abbracci e Baci”,
vi ritrovate clienti di qualcuno senza che vi siate accorti di niente. O
peggio ancora, siete le vittime di truffatori in perfetto stile Vanna Marchi
& Co. Queste persone esistono amici… e credere di esserne immuni è
un’illusione che potremmo stare già ora pagando molto cara! E adesso vengo finalmente al cuore
del messaggio che vorrei trasmettere. La ragione per cui ho parlato di Cuore, è
che un campo dove la manipolazione trova oggi grande applicazione, è proprio
quello delle pratiche per la crescita interiore e la guarigione spirituale.
E se è vero che l’attrazione verso i mondi sottili è una forza potentissima che
permette di esplorare, conoscere e salire presumibilmente sempre più in Alto,
dobbiamo però ricordarci che viviamo
sulla Terra, e sulla Terra i nostri piedi devono rimanere, altrimenti rischiamo
di volare via insieme al vento e agli eventi, perdendo la Connessione più
importante: quella con la nostra Volontà. I venditori di spiritualità non
vogliono il nostro Cuore, quello è, e rimarrà (per fortuna),
sempre nostro. I venditori di spiritualità arrivano da fuori, e fuori restano,
ma agendo con strumenti di natura energetica, psicologica e tramite tecniche
manipolative del linguaggio, rischiano di determinare in noi grossi danni,
interrompendo il nostro vero e più profondo percorso interiore. Loro vogliono solo il nostro valore
materiale, ovvero il nostro denaro o il nostro servizio
gratuito, e per ottenere ciò, lavorano
in modo scientifico per offuscare la nostra Mente. E bada bene amico mio,
con certe persone avrai sempre l’illusione di essere stato tu ad offrire, tu a
decidere di partecipare ai seminari, alle sedute energetiche, ecc … Ma si
tratta di una languida nebbia in cui ti hanno immerso attraverso la magia della
fascinazione, ovvero la capacità di far
sì che ai tuoi occhi essi, essi stessi (i venditori), appaiano come amici
salvatori, guru più unici che rari, l’occasione per te di crescere
interiormente, trovare finalmente la felicità. Tu non ti accorgi o fai finta di non
accorgerti, che di fronte a certe domande, o a certe considerazioni, costoro si
comportano in modo sfuggevole, arrogante e perfino vagamente violento;
non ti accorgi che quando qualcuno si avvicina alla fortificazione dogmatica
che si sono costruiti intorno, reagiscono tacitando l’ignaro ribelle, con
evidente eccessiva durezza, con il solo intento di mantenere la propria
immagine intatta, agli occhi degli altri clienti-discepoli riuniti in cerchio.
Questo significa essersi fatti rubare il senso critico: tu smetti di giudicare,
perché giudicare non è proprio di chi vive nelle “alte sfere” o ambisce ad
esse… dove si vibra a più elevate frequenze. Ricomincia, allora, ad osservare amico mio, giudica il tuo guru, non è
un peccato… e chiediti se non possa trattarsi semplicemente di un qualsiasi,
sebbene scaltro, squallido venditore di illusioni! Nelle
cerchie dei sedicenti discepoli di questi sedicenti maestri spirituali, si
possono ritrovare persone perfino felici di aver perso il lavoro (perché questo
magari faceva parte della “terapia”); felici di pagare tanti soldi per terapie
energetiche inutili o addirittura dannose, seppur magari strabilianti (perché
facenti uso di giochetti “magici” d’effetto); felici di bruciare settimane per
regalare il proprio servizio e il proprio tempo, a guru che vivono nelle
comodità e perfino nel lusso. Questi venditori senza scrupoli
mentono sapendo di mentire, pianificano al pc, usano i social, si promuovono –
sempre tra le righe – addirittura come maestri spirituali, sgranando
inverosimili rosari di esperienze mistiche ed energetiche al limite del divino,
lavorano in modo cesellino sui singoli malcapitati, per creare intorno a sé una
cerchia di pseudo-discepoli, per lo più divisi tra loro (o ignari gli uni degli
altri) ma ognuno singolarmente connesso al guru, il cui unico ruolo nel gioco,
è invece quello di essere clienti privi di senso critico, incapaci di
retrocedere, quasi paralizzati di fronte al potente gesto del
mago-guru-venditore. Ma
se un mercatante ti infila nel sacchetto tre mele marce e una buona, il danno è
piccolo, ed è solo materiale. Se invece stavi cercando le risposte alle “grandi
domande”, se cercavi veri amici, se cercavi l’amore perduto nei labirinti della
fredda società, allora rischi grosso,
perché i venditori di spiritualità ti lasceranno intrappolato in una confusione
ancor più perfida, una lucrativa (per loro) ritracciatura del tuo percorso
spirituale, una semplificazione della tua mappa interiore, che viene
inserita nella matrix della loro piccola aziendina familiare, costruita magari
su metodi terapeutici e costrutti teorici, inventati a partire da parole chiave
di moda, lette nei best seller del momento. Ecco
amico mio, come il potere di gestire le
energie sottili, se usato da persone spregiudicate, può determinare grandi
danni in chi si fida. Se vuoi capire che cosa ha inteso fare una persona di
questo tipo che hai incontrato sul tuo cammino, cerca allora di osservare, in
modo obiettivo, quello che costei ha realmente fatto e le conseguenze su di te,
indipendentemente dal fumo che ti sta gettando negli occhi. Non diamo le chiavi della nostra
Mente e del nostro Cuore, a chi cerca di ammaliarci con la “manipolazione”, al
solo scopo di lucrare su di noi per brama di denaro, per
follia, per egoismo… e chissà per quali altri bassi scopi.
Articolo di Mauro Vanzini (Fisicaquantistica.it) |
LISTA ARTICOLI
- L'UNICO VERO CORPUS HERMETICUM
- COMMENTO ALL'INNO AL SOLE DI GIULIANO KREMMERZ
- L'INNO ALLA CARITA'
- CHE COSA E’ LA FRATELLANZA TERAPEUTICO MAGICA DI MYRIAM?
- TRATTO DALLA CORRISPONDENZA DELLA NOSTRA SCHOLA
- LA COSCIENZA CHE DIVIENE AMORE DI DIO
- UN OMAGGIO AL MAESTRO GIULIANO KREMMERZ
- LUZ, IL NOCCIOLO DELL'IMMORTALITÀ
- ESEMPI DI PRUDENZA E SAGGEZZA
- LA DIMENSIONE TRASCENDENTE È IL CULTO DIVINO.
- DAL LIBRO I FONDAMENTI SPIRITUALI DELLA VITA DEL FILOSOFO VLADIMIR S. SOLOVIEV
- APPENDICE AL TESTAMENTO SPIRITUALE DI SALVATORE MERGÈ SULL’ "ALCHIMIA MATERIALE"
- PREGHIERA A MARIA
- LE MOTIVAZIONI CHE INDUSSERO GIULIANO KREMMERZ A ESCLUDERE I MASSONI DALLA NASCENTE E FUTURA FR+ TM+ DI MYRIAM.
- GALILEO ALL'INFERNO
- CONSIDERAZIONI FRATERNE
- IL VIAGGIO DI DANTE ALLA LUCE DEI RIMANDI ASTRONOMICI
- UN PENSIERO DI RINGRAZIAMENTO PER IL TESTAMENTO SPIRTUALE DEL M° SALVATORE MERGÉ
- LETTERA DI RINGRAZIAMENTO A FIRMA DI UN FRATELLO DI HERMES
- NOTIZIA STRAORDINARIA !!!
- KHEPRI
- LA PICCOLA CORONCINA PER LA DIVINA PROTEZIONE
- CURIOSITA' ASTRONOMICHE
- IL GENIO
- IL PENSIERO
- E NON CI INDUCA IN TENTAZIONE
- LETTERA A S.S. PAPA FRANCESCO
- MISURARE IL TEMPO IN CHIESA CON IL SOLE
- LETTERA DI RINGRAZIAMENTO E ALCUNE RIFLESSIONI SUL TESTAMENTO SPIRITUALE DI SALVATORE MERGÈ
- IL CUORE
- IL TERZO OCCHIO LA GHIANDOLA PINEALE O EPIFISI
- SIMBOLI DEL CUORE DI CRISTO
- LA BOCCA: LA PORTA DEL TEMPIO
- I MISTERI ISIACI
- ISIDE REGINA
- PREGHIERA A ISIDE
- LA LEGGE DELLE LEGGI
- COMUNICAZIONI
- ALMANACCO 2018
- INNO AL SOLE
- GENIO DI LUNA
- THOTH
- IGNIZIAZIONE: IL VALORE DELLA PURITÀ
- LA TAVOLA ZODIACALE - SECONDA PARTE E FINE
- LA TAVOLA ZODIACALE - PRIMA PARTE
- MACROCOSMO E MICROCOSMO
- SIMBOLISMO DEGLI ANIMALI SACRI DELL'ANTICO EGITTO
- ASTRONOMIA AD OCCHIO NUDO
- KEPLERO IL PREVEGGENTE
- ILLUMINAZIONE ... VENDESI